Fractions are important because they are so much a part of our adult world and adult way of thinking. Yet, as ubiquitous as they are, it is not easy for young students to learn how to calculate with fractions. It can be difficult for parents and teachers to understand the multiple areas of difficulty when young children begin to conceptualize fractions.
Fractions are Part of Everything
We measure amounts; length, area, volume, temperature, precipitation, fuel, money, and energy in terms of whole units or fractional parts. We use fractions to track athletes, sports, time, weight, precipitation, and investments.
Fractions abound in everyday language; half baked, six of one, piece of cake, split in two, double or nothing, a large part of, slim chance, whole is more/less than the sum of its parts, dime a dozen, the whole nine yards, and so on. Other idioms rely on the same kind of proportional understanding that is so important when thinking about fractions; tempest in a teapot, an ounce of prevention/ as compared with/ a pound of cure, a stitch in time, not playing with a full deck (one sandwich short of a picnic and all these lovely idioms), see eye to eye (one to one), well begun is half done, or once in a blue moon. We don’t do anything by half!
When we make comparisons we are often engaging in the same kind of reasoning that requires understanding whole/part relationships. Words such as small, minute, tiny beg the question; how small? How minute? How tiny? And, compared to what?
Fractions are important because they are central to more advanced mathematics and scientific pursuits, as well as to understanding details influencing current events, concepts of healthy living, and citizenship.
Which is more one-quarter or one-third? Well, as simple as this sounds, many people seemed to have gotten confused when deciding which burger was a better deal.
Difficulties Conceptualizing Rational Numbers Or Hang on, you mean every number can be written as a division problem?
Even ‘good’ math students have trouble understanding fractions. Some of this is due to the fact that they have to spend mental muscle conceptualizing new ideas and vocabulary. Also, when learning about fractions students have to rethink concepts that they thought they already understood.
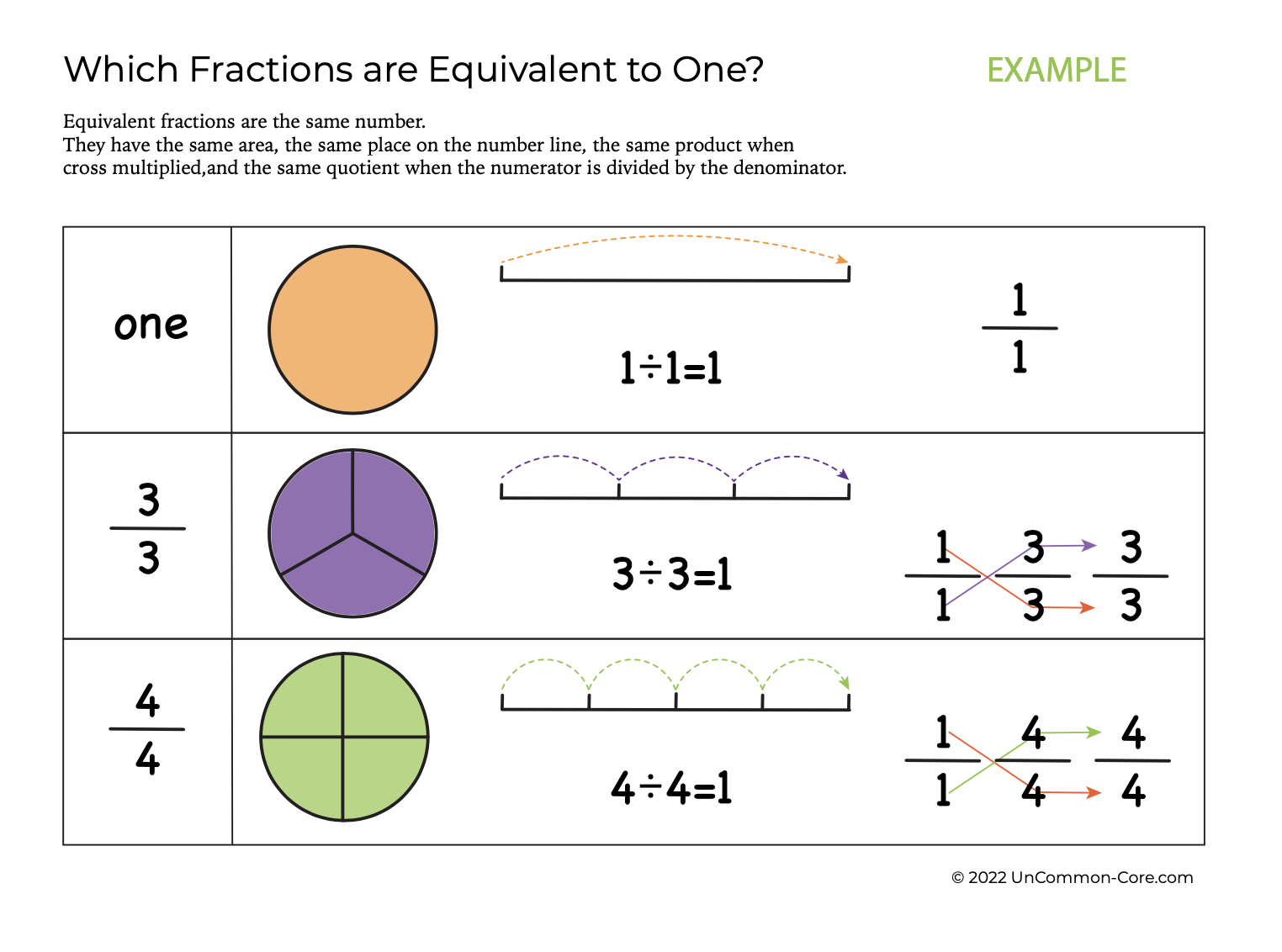
Ratios are an entirely novel idea to young children who have only just learned to count. Students are familiar with integers that each occupy a unique, discrete place on the number line. Integers do not bump into each other. They do not pile up on top of each other. Yes, they go on and on forever, however there is still space between them. And, there is the same amount of space between each of them. Once you get the hang of it, it is easy to tell which integers are bigger or smaller than the others.
Now it turns out that there is an infinity of numbers in between each integer – fractions are jam packed together – yet there is always room for more numbers between each fraction. The number line turns into a long and elastic mathematical model.
With the introduction of rational numbers, students have to re-evaluate everything they thought they knew about numbers. Whole numbers, natural numbers, and integers can all be thought of and written as ratios!
Every number with a numerator and a denominator can be thought of as a division problem. Students are in the habit of thinking of numbers as amounts, or values. Reconceptualizing numbers as proportions or ratios will take a lot of time and effort. Rather than thinking of a number as a line of pebbles, we think of rational numbers as the proportion between two lines of pebbles.
Furthermore, any two lines of pebbles that have that same relationship are the same number.
Even worse, familiar operations start acting goofy. Once friendly, reliable, addition and subtraction have become complicated by pesky denominators.
In integer-world, multiplication yields a larger amount. In fact, that is one of the ways that students are taught to check their work – if they multiply 7 by 8 and get a small number they know to check their work. Many students will have made the generalization into a kind of pseudo math rule. Kids expect the product to be larger than the numbers multiplied. However, as soon as rational numbers are tossed into the mix, we can multiply 7 by 1/8th and get a strange answer – 7 eighths. Not only is
multiplication upside down, division suddenly yields larger numbers than before. What’s a kid to do?
Learning about fractions introduces new vocabulary, yet it also causes students to question and rethink familiar vocabulary. Students must expand the way they think about terms such as multiplication and division to explain what happens when fractions enter the equations. Some students may have been using terms such as ‘integer’ and ‘number’ interchangeably. They will have to update their understanding of ‘integer’ and ‘number.’ Also, kids familiar with the word ‘rational’ might think of it as ‘the opposite of crazy.’ Suddenly ‘rational’ comes from ‘ratio’ and everything gets ‘crazy.’
Students who were already having trouble with math find fractions even more problematic. In order to successfully manipulate fractions, students have to have a deep understanding of equality, comparison, proportionality, and place value, as well as addition/subtraction and multiplication/division. Students without these understandings or students who haven’t had time to build their number sense into a flexible network of numerical connections, will have even more difficulty understanding fractions.
Fractions are difficult to teach for several reasons. Teaching fractions introduces ideas that shake up everything kids have learned about math so far. There are a lot of significant ideas which students will have to reprocess in order to learn about fractions such as, comparison, equivalency, vocabulary, advanced rules for addition/subtraction and multiplication/division and symbolic representation. Pulling mathematical ideas from real life models becomes more detail oriented and more complex. The concepts related to understanding fractions – equivalence, mixed numbers, numerators, denominators, decimals, percents – cannot be presented all at once, yet each impacts the others, extending the complexity of studying rational numbers. Since children are not able to explain why it is so difficult for them to conceptualize rational numbers, teachers must anticipate challenges and ameliorate these difficulties on their students’ behalf.
What can Teachers Do?
There are a number of things teachers can do to make learning about fractions easier for all students. Just being aware of how complicated fractions seem from a child’s point of view is helpful.
While math teachers rarely think of ourselves as language teachers, when it comes to fractions, ratios, proportions, and percentages, math students can get a big boost from describing mathematical concepts in plain English (French, Dutch, Turkish…).
When introducing content that will require your students to conceptualize ideas they have already learned, let them know what kind of new thinking is required. For example, when talking about division with fractions, make note of the new thinking which is required (the quotient might be larger than the dividend). Explicitly contrast this new way of thinking with the students’ familiar ways of thinking about division. Then demonstrate how both division problems are asking the same
question (how many times can we subtract the divisor from the dividend?) except the answer is different because when the divisor is a fraction, the quotient will be larger. Provide numerous examples to help your students recalibrate their understanding of division.
Use as many kinds of mathematical manipulatives as possible over the course of the year. Start small with simple examples. Then, as your students’ understanding grows, bring in more complex manipulatives for students to explore.
Leverage what students already know about everyday language, art, and music, when introducing similar concepts having to do with fractions. Introduce one novel idea at a time and provide many situations in which students can get a new perspective on that new idea. Continue to give students opportunities to build concepts by relating fractions to other math/science subjects as they are studied throughout the year (time, measurement, charting progress (spelling, math facts, PE…), and gather a team of other people who can help your students explore and consolidate the ideas they are learning.
Specialist teachers can be some of your biggest allies when teaching fractions. Reading interventionists or ELL teachers can review comparative language and related key concepts such as equivalence, whole, part, and other vocabulary. Music teachers can help students connect fractions with musical notation, time signatures, tempo, and octaves. Art teachers can give students new perspectives on proportion, scale, and other concepts related to fractions. PE teachers can help students collect information about themselves that can be expressed in ratios and they can help students conceptualize magnitudes of distance, time, and speed. Since fractions are part of everything, invite specialist teachers to help teach your students about them.
Parents can also be a huge help when it comes to teaching their children fractions. Students can cook, shop, or discuss current events with their families. Parents can bring fractions into conversations, games, and events that are taking place in real time. Kids can practice their new skills and vocabulary at home. When parents teach fractions at home, students can see how important and ubiquitous fractions are. Parents who speak languages other than English can make sure their children learn to talk and think about fractions in multiple languages.
Finally, in the words of Winston Churchill, “Never give in.” Remind yourself and your students that manipulating fractions is difficult but worth the effort. Like anything else that is challenging, it will take longer than you think to get it right and it will be easier if you find ways to play with it.
Share This Story, Choose Your Platform!
Download Colorful Collections:
A Mindful Exploration of Proper Fractions
Help your students make sense of fractions.
I started teaching in 1987, which means I’ve collected many tips and tricks along the way. In this ebook, I share concepts, strategies, and classroom materials to help you make math sticky.
Along with this useful ebook, you will receive weekly emails from StickyMath@UnCommon-Core.com. I send information like: teacher tips, educational ideas, book reviews, curated lists, reviews of educational sites, and free first drafts of products that I’m creating for my TPT store. That way, you get helpful ideas and free stuff, while I get some feedback before I finalize products and put them up for sale.
I value your privacy. I will never sell your information. You may unsubscribe at any time.
All the best!
Isabelle
Isabelle Hoag M. Ed.

