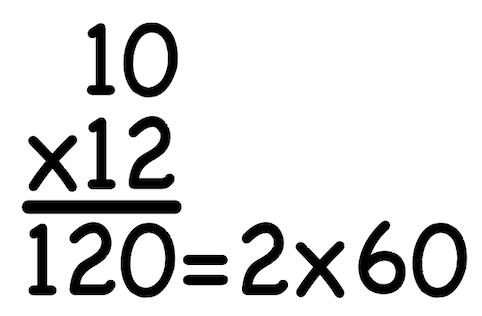
Greatest Common Factor and Least Common Multiple Are Two Sides of the Same Coin
The largest factor that two numbers have in common can be multiplied by the smallest number which can be divided by either of the pair to give the same answer that results when that pair of numbers is multiplied together! YES, this is a nifty numerical relationship. It also illustrates how fractions are complex.
Actually, once your students start sorting through the prime factors of the original pair of numbers, the reason behind this complex relationship becomes clear.
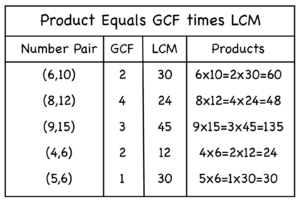
This general relationship will help your students make sense of why prime factors are so useful in mathematics. Here is an activity which will illustrate what is going on behind the pattern:
Explore the Relationship
Encourage your students to list the factors of both numbers in any pair of numbers.
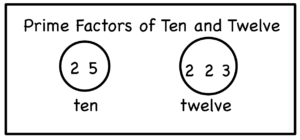
Identify the greatest common factor GCF which is just what it sounds like~ the largest factor shared by the two numbers. It doesn’t have to be a prime number, but it will be made by multiplying whichever primes the two numbers have in common.
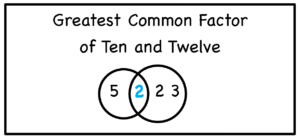
Now, have your students sort through the prime factors again. This time have them match up the prime factors, combine any duplicates, and multiply to find the least common multiple LCM.

After finding GCF and LCM for several pairs of numbers, students will start to see why their product is the same as the product of the original pair. The prime factors used to determine the GCF are excluded from the calculation for LCM. This is why, between the two of them, all the prime factors are represented only once ~ as if each is the flip side of the same coin. It is also why the product of GCF and LCM is identical to the product of the original pair of numbers.
But Wait! There’s More!
Understanding prime factors is an essential math skill your students need in order to be able to add and subtract fractions with unlike denominators. Students will need a lot of thoughtful practice and reflection in order to understand the concept.
However, there is a way to introduce adding and subtracting with unlike denominators without even mentioning prime factors! This super simple adaptation will allow your students to become familiar with the big ideas behind adding and subtracting with unlike denominators without having to take in too much new information all at once.
There is a subset of this general relationship that makes adding fractions with unlike denominators more straightforward. Before you even mention prime factors to your class, you can introduce your students to adding with unlike denominators by making sure to use number pairs that follow a simple rule.
When the Difference between Unit Fractions Equals the Least Common Denominator
Wait! What? Can the difference between unit fractions equal the least common denominator LCD? How could that happen?
There is a very special group of number pairs that can be used to make finding the LCD much easier. These pairs are easy to identify: the difference between them is equal to their greatest common factor.
Take a look at (8,12).
The difference between 12 and 8 is 4.
Four is also the greatest common factor of eight and twelve.
When the difference between the two numbers is equal to their GCF, their least common multiple LCM is the same number as their least common denominator LCD ~ when the pair is used as denominators while adding or subtracting fractions.
This sounds complex, but an example will help.
Share This Story, Choose Your Platform!
Download Colorful Collections:
A Mindful Exploration of Proper Fractions
Help your students make sense of fractions.
I started teaching in 1987, which means I’ve collected many tips and tricks along the way. In this ebook, I share concepts, strategies, and classroom materials to help you make math sticky.
Along with this useful ebook, you will receive weekly emails from StickyMath@UnCommon-Core.com. I send information like: teacher tips, educational ideas, book reviews, curated lists, reviews of educational sites, and free first drafts of products that I’m creating for my TPT store. That way, you get helpful ideas and free stuff, while I get some feedback before I finalize products and put them up for sale.
I value your privacy. I will never sell your information. You may unsubscribe at any time.
All the best!
Isabelle
Isabelle Hoag M. Ed.

