Why Do Whole Numbers Have a Denominator of One?

Learning about Fractions Requires a New Look at Whole Numbers

Many students are surprised when they discover that whole numbers have a denominator – let alone that said denominator is  always one. It is essential for students to understand why whole numbers have a denominator of one in order for them to find equivalent fractions, place fractions and mixed numbers on the number line, and calculate with fractions or mixed numbers. If your students cannot explain why whole numbers have a denominator of one, then they don’t understand denominators in general.

Start with Vocabulary

Denominators tell how many unit fractions fit perfectly between zero and one. They show how many equal size hops are needed to move from zero to one on a number line. They show how many same size measures are needed to move from zero to one on whatever scale you are using. For this reason, students need to work with fractions of length, area, volume, duration, and weight, in imperial and metric units, in order to grasp the full meaning of ‘denominator’. 

Denominators name fractions. The number of equal size pieces that fit perfectly between zero and one is:

• the name of the fraction. 
• the number in the denominator.
• the numeral under the ‘fraction bar’ or vinculum. 

Equivalent Fractions share a place on the number line. When fractions are equivalent to a whole number, the numerator will be a multiple of the denominator. 

Fractions are numbers that may, or may not, fall between whole numbers on a number line. They are rational numbers that express a relationship between the numerator and denominator. When whole numbers are written in fractional form, they have a denominator of one, meaning that on the scale being used, whole numbers represent an entire single unit of whatever is being measured. There are an infinite number of fractions between each pair of sequential whole  numbers.

Numerators tell how many unit fractions were used to make the number. Three-fourths is understood to equal one-fourth plus one-fourth plus one-fourth, or in other words, 3 one-forth size pieces. Twelve-twentieths describes a dozen one-twentieth size pieces. 

One represents a single item or object. It is the first whole number to the right of zero. The word, ‘one,’ came into English from old Germanic languages. It is cognate with ‘een’ in Dutch, ‘en’ in Norwegian and Danish, and ‘ein’ in German.

However, when we look at the word for ‘one’ in Latin and romance languages, we catch a glimpse of  another function for this term.  In Spanish and Italian ‘one’ is ‘una’ or ‘uno’, in French it is ‘une’ or ‘un’, in Latin ‘unus’, and in Romanian ‘unu’. These words are cognate with the English word, ‘unit,’ as in an undivided whole or a standard of measure.

Rational Numbers include fractions, ratios, decimals, and percents. Rational numbers show relationships. We can squeeze as many rational numbers as we want in between two sequential whole numbers. Number lines that show rational numbers are more like rubber bands than rulers. 

Unit fractions are the standard unit of measurement for rational numbers. Five-halves is understood to be equal to 5 pieces, each of which is one-half of the size (weight, volume, area, length, duration, radius, temperature, saturation, height . . .) of one complete item of whatever is being measured. Make sure your students can explain why unit fractions with larger denominators are smaller size pieces. 

Whole numbers start with zero and continue forever, one step at a time. There is a distance of ‘one’ between each whole number, regardless of the scale being used. One is the first number to the right of zero on the number line. Whole  numbers continue forever, yet the space between them is always the same. A line of whole numbers can be thought of as a yard stick that keeps going for ever; no matter how long it gets, it will never stretch, the span between each number remains constant.  The distance between Six and seven is the same as the distance between 256 and 257, and the distance between zero and one. That distance is called ‘one whole’.

Young Students’ Concept of ONE

The number ONE represents a single thing. These single objects have many different sizes. We teach young students that whole numbers represent complete, undivided items – which can be counting regardless of their size or differences. When we ask, ‘how many animals,’ every single animal is assigned the same value; from gerbil to giraffe each animal counts as ‘one.’ One whole refers to a complete circle or sphere, an entire acre of land, or a full bottle of water. Whatever the object is ~ a century, a dozen, a pair, a dollar bill ~ when we call it ‘whole,’ that means nothing has been removed or added. 

Until rational numbers came along, the ‘size’ of each ONE didn’t matter to students due to the fact that whole numbers are equally spaced along the number line. Whole numbers are each ‘one step’ away from their immediate neighbors.

Many Different Ones

Adults on the other hand, have more experience with the concept of  ‘one’.  We would never expect currencies in various countries to have the same value, whereas when elementary students see a 1, they expect that it will be equal to all other ones. Yet, this idea of ONE is only true when we use numbers to count. When we use ONE as a unit of measure,  its ‘size’ depends on what is being measured and which scale we are using to measure it.

Each of the fractions below is one less than the whole number; yet, they are all in different places. Ten-tenths minus one-tenth is nine-tenths. Nine-ninths minus one-ninth is eight-ninths. Eight-eighths minus one-eighth is seven-eights and so on. This is due to the fact that each of them is counted by a different standard – a different ‘one’.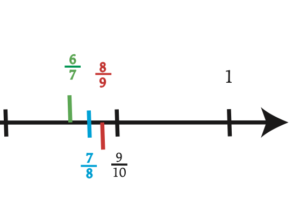

When anything is measured in numbers, we use ONE of those things to evaluate a group of them. Thirty-two dollars is understood to mean 32 individual one dollar bills or the equivalent. We use unit measures all the time: one hour, one centimeter, one mile, one cup, one liter, or one square meter. Adults know that one degree Celsius is the basic unit by which temperature is measured on that scale. We also understand that a single degree on the Celsius scale will measure a different amount of heat than one degree on the Fahrenheit scale.

It is important to unpack these ideas about one as a unit of measure, so that students can think flexibly about which ‘one’ is being measured. First we teach students to think of  ‘one’ as measuring an amount ~ one giraffe is equal to one mouse when you are counting how many animals there are. When learning about fractions, it’s time for students to differentiate various types of ones ~ one-half of an hour is a lot more time than one-sixth of an hour, or than one-half of a minute

Young Students’ Concept of Number Lines

How did you figure out the name of the number in the graphic? You counted by ones to move from zero to six. On the whole number line, once you know where zero is, you can figure out where the other numbers belong by counting. This is because you have extensive experience using a number line to determine the size of whole numbers.

Now imagine what a young student might think when they first encounter the number line.

On the number line for whole numbers, there is no place to land in between numbers.

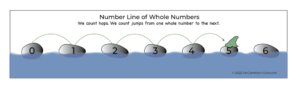
How do you explain to young children, who are accustomed to pointing and counting objects, that the first stone/number is not counted? You could say that the ordinality of the stones does not match their cardinality. However, I don’t think that would help a little kid. Instead, we tell children: 

Green Froggy sits on the first rock all day basking in the sun and snacking on flies.

The first rock is Green Froggy’s home base. Green Froggy’s home base is called ‘zero’. We do not count Green Froggy’s home base.

In fact, (are you sitting down?) we are not even counting rocks! We are counting ‘Froggy hops’ from one stone to the next.

Green Froggy leaps from zero to one in a single jump.

Use the Number Line to Help Students Make Sense of Denominators

How does the number line change when rational numbers are included? Suddenly, there is as much space as needed between each number. You can place as many fractions as you want between any two numbers! Also, equivalent fractions share a place on a number line. When rational numbers are included, there are many ways to name each place on the line.

One of the strangest changes when rational numbers are included in a number line, is that there are many different kinds of  ‘ones’. The distance between sequential whole numbers is the largest ONE. Half of that distance, one-half, is the next largest ONE. 

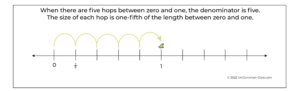
Yellow Froggy needs five leaps to move from zero to one.

Each of Yellow Froggy’s hops is one-fifth of the distance between zero and one.

So one-fifth becomes the standard unit of measure for any distance that Yellow Froggy travels.

Later, After hours of  Experience, Conversation, Explanations, and Consideration ~

Students will eventually realize that the denominator of any number expressed in fractional form is the number of equal hops between zero and one.  Whole numbers have a denominator of one which shows there is one entire, complete hop between zero and one. The unit fraction for whole numbers is one over one. One over one is the only unit fraction that is not a proper fraction. Hmm, what a great segue to teaching improper fractions. 

Make sure your students can explain why whole numbers have a denominator of one when written in fractional form. With this key bit of information, switching numbers from improper fractions to mixed numbers is much easier to understand.