Colorful Squares

Learning about square numbers helps students develop their understanding of number patterns and the relationships between geometry and algebra. It also gives students practice with sequential patterns and multiplication facts.

The Colorful Squares activity can be done as a stand alone project to increase students’ number sense, vocabulary, or logical thinking skills. It can also be done as part of a larger thematic unit on square numbers, area and perimeter, multiplication, or investigating number patterns.

This is the kind of creative exploration that fosters students’ excitement for math and provides them an opportunity to build connections between shapes, numbers, and patterns. Number sense, that deep, automatic understanding of how numbers relate to each other and the real world, takes time to develop. Colorful Squares and similar activities invite students to revel in discovering hidden patterns in math, engaging their imaginations as well as their logical thinking while expanding their mathematical thinking and giving them a worthwhile project on which to practice math skills.

Preparation:

 Identify academic standards and learning goals to give meaning and direction to your students’ work. Based on the standards and learning goals, decide how to gauge your students’ progress.

Plan a series of lessons to give your students ample time and support as they work toward the learning goals. Remember to schedule some extra time due to the hands-on nature of this activity. Decide if you want your students’ squares to follow the colors of the rainbow. If so, make plans ahead of time.

If your students meet with other teachers, you may want to share what you are doing with those teachers, too. Art or science teachers may have rainbow related activities which would coordinate with making Colorful Squares in math. The music teacher may have fun songs about colors. Reading, ESL, and math interventionists might want to find ways to support their students’ work. Foreign language teachers may use the opportunity to review names of colors or numbers.

Gather the materials that you would like your students to use. These could include colored pencils, crayons, or highlighters, rulers, scissors, glue, blank copy paper or grid paper. You might need some paper clips, folders, or baggies to store materials between lessons. Have extra materials and supplies ready in case of accidents.

You may decide to provide construction paper as a background for arranging squares after they have been cut out. Consider using colorful paper to print copies of different size square grids to make ready-to-cut handouts. This is an easy way to have the colors in the order of the rainbow when the squares are arranged by size. Print larger grids for students with vision or fine motor challenges.

Activity Ideas:

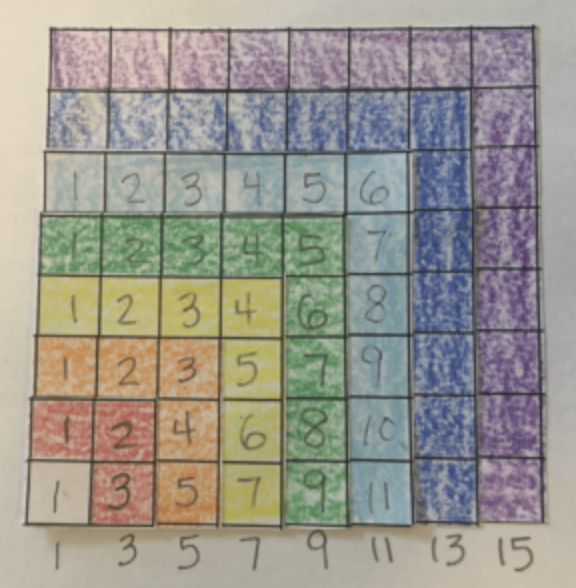
 One way to begin is to have your students color squares of different sizes on graph paper. Students can then cut out the squares and put their initials on the back of each one. Invite them to arrange their squares by various criteria in order to discover patterns. You might want to have a discussion to collect various ways that students could sort their squares:

• by size
• by the order of colors in the rainbow
• alphabetically by names of colors or numbers
• warm or cool colors
• parity – is the number of cells in each square even or odd?
• by lining them up side by side
• by stacking one on top of another

What do your students notice as they organize their squares? Do they have a complete set or could some be missing? How can they use the developing pattern to figure out if some squares are missing? Help your students pay attention to what they can learn by sorting them in different ways.

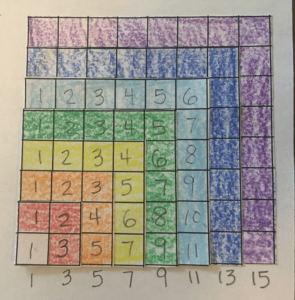
Another way to begin would be to copy squares or grids directly onto colorful paper or card stock. Students could tell if they have a whole set by looking at the color of the paper rather than by noticing gaps in the pattern.

Instead of opening with individual or small group work, your students might benefit from a whole class conversation introducing the sequence of square numbers. You can model how to search for patterns by ‘thinking out loud’ as you bring your students’ attention to various attributes of interest.

One way to make the activities more complex is to invite students to record their ideas, puzzles, questions, and conclusions as they do their work. This would mean that every so often, the students who accept the challenge would pause and write notes in their math journal to keep track of what they are thinking as they work. These notes could be in words or pictures, sometimes a doodle is enough to remind us of what we were thinking at the time. Let students decide for themselves if they want to accept this note taking challenge.

There are many ways to make the activities more complex. You could encourage some students to use more squares or work with larger numbers. The questions that you ask students about their thinking and their work could lead them into more challenging directions.

Make the activities easier by having students work in pairs or small groups. You might invite parent helpers into class and give them instructions on what kinds of support they could offer without taking over the project from the students. Another way to make these kinds of activities easier is to review important vocabulary and ideas with the students ahead of time. This helps prepare the students for the kinds of thinking and questioning that they will be doing.

Plan extra time for students to play, yes play, with the materials they will be using in math class. Invite young students to imagine each square as a house. Obviously, each house needs a triangle roof. Given more grid paper, how will your students go about creating triangle ‘roofs’ that fit on top of each square? Encourage your students to includes quares, grids, & triangles in creative projects to give them more experience manipulating squares, collecting data about how squares fit with each other and with other shapes. This inventive ‘messing around’ is essential learning time needed to familiarize students with the materials they will soon be using in more academic pursuits.

Many and Various Directions

 Which mathematical concepts would you like your students to connect with square numbers? Keep your chosen academic standards in mind. Post the learning goals for your students where everyone can see them. Refer to the learning goals often so that students get into the habit of comparing what they are doing in class and how their work will be assessed to the learning goals on display.

In order to get the most out of any colorful squares activities, students must be comfortable using academic vocabulary such as, grid, cell, row, column, vertical, horizontal, and diagonal. Review essential vocabulary frequently. Provide examples and counterexamples for specific mathematical terms that are used in class. Model the vocabulary that you expect your students to know. Spend part of language class investigating mathematical vocabulary. For example, you may want to have your students create Vocabulary Sunrise mini posters connecting words like vertical, vertex, & vertigo with their Latin root vertex or ‘highest point.’ Help your students connect vocabulary with mental images; join up the phrase ‘squaring a number’ with images of making actual squares.

If multiplication or square numbers are new for your students, it is important for them to explore the relationships between the multiplication facts and the square shapes. Remind your students that multiplication facts can be pictured as height times the width of rectangles. When they see the math fact 6 x 4 = 24, they could say, “Six by four is twenty-four.” Squares are special rectangles in which the height and width are the same number. You might invite your students to write a multiplication sentence to go with each square, or highlight the square numbers on a multiplication chart. Until they understand that a four by four grid made up of sixteen cells is a different way of explaining that 4 x 4 = 16, your students will have difficulty with more complex investigations.

Encourage students to find other shapes or items to use when creating arrays of square numbers. They could arrange coins, star stickers, dots, or fingerprints into arrays that illustrate square numbers. An array does not have to be made of squares or tesselating shapes.

Would you like your students to consider how colorful squares can be used to explore the concepts of area & perimeter? First make sure they calculate area and perimeter correctly. Area is calculated and expressed in unit squares. Perimeter, however, length – a two dimensional line – that describes the edge of a shape and is expressed in units of length.

Encourage students to look for patterns in the way that area & perimeter grow as the squares increase in size. They could make graphs, charts, or mini-posters to share what they discovered or to explain the process they went through while searching for patterns. Ask students specific questions such as, ‘how will the sides of the squares grow as the sequence continues?’ Any way they approach the question, your students will gain meaningful experience finding the area and perimeter of squares.

Number patterns are essential to math. They help us see relationships and identify recurring motifs. Recognizing the underlying structure of mathematics helps students solve novel problems by being able to figure out which familiar strategies are most likely to work in new situations.

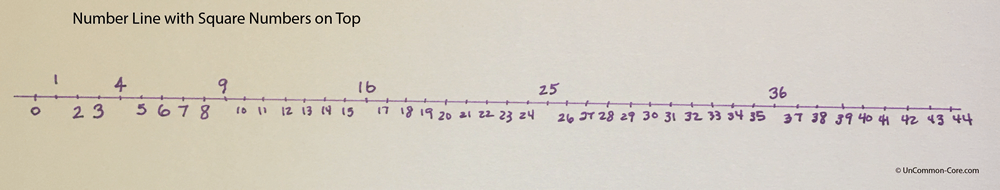
Searching for patterns is fun, and exciting, and educational. Plus, kids get lots of math practice.

What kinds of number patterns could your students find when looking at consecutive squares?

• Height times width equals the number of cells in the grid
• The bases & sides of sequential squares increase by +1
• The perimeter of sequential squares increases by +4
• Consecutive square numbers alternate between even & odd
• Squares of even numbers have an even number of cells
• Squares of odd numbers have an odd number of cells
• The difference between consecutive square numbers is the series of odd numbers
• What other patterns could they find?

The Series of Odd Numbers Hidden in the Squares

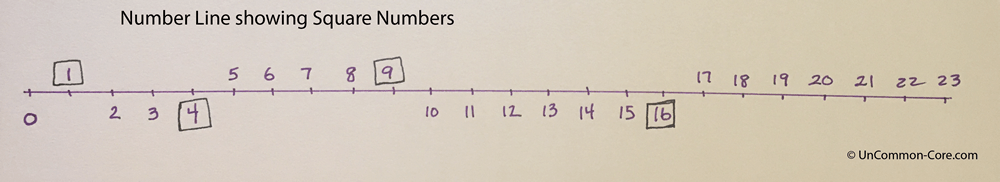
One +3 is four. Four +5 is nine. Nine +7 is sixteen. Sixteen +9 is twenty-five. Twenty-five + 11?

The difference between sequential square numbers is the series of odd numbers. Seriously, how cool is that?

Plan an activity to place this mind-boggling pattern directly in the path of your junior mathematicians as they sort their paper squares. For example, invite young students to mark the square numbers on your class number line, then get them started counting the numbers between squares or calculating what number must be added to get from one square to the next.

You could ask specific questions. Are there any patterns between square numbers? How could you find a pattern in between the square numbers? What happens if you look at the difference between each square number and the next one? Students could approach any of these questions in at least two different ways. They could subtract to find the difference between consecutive square numbers. Alternatively, they could count the number of cells needed to build the next larger square. Encourage your students to find their own ways of working. Then give them time to share what they discovered and how they figured it out.

Square Numbers as the Sum of Consecutive Odd Numbers

Any Square Number can be written as a sum of consecutive odd numbers. Wait, what?

We are most familiar with thinking of square numbers as the product of a number times itself. We march up the number line squaring each digit in order to create the sequence of square numbers. However, that is not the only way to calculate the series.

We can also generate the series of square numbers by adding sequential odd numbers together. Starting with one, which is the first square, then adding three to get the next square and so on.

While this pattern may seem surprising at first, it is basically the same pattern as above, just described in a different way. Challenge your students to look for other methods to describe this relationship between the series of odd numbers and the series of squares.

Reflect and Share

 It is important to give your students time to consolidate their understanding and wrap up the activity. This provides an opportunity to review what they have done. Students could create a chart to show what they have learned about the number patterns involving square numbers. They could write about their understanding in their math journals. They could give short presentations to the class or to their math group.

You might want to snap photos of student work to document their new understanding. If you create learning portfolios for your students, let them write captions and comments to include with the photos. Alternatively, create a display from their work, showing your students how excited you are by their discoveries and giving everyone another chance to revisit the work.

As your students reflect on what they have learned, you have the chance to assess your students’ progress. How well did each student do in terms of the learning goals? What – if any – remediation is needed? For whom? Then what? This is also a perfect moment for you to reflect on your teaching practice and make note of ideas for the next time you teach this or similar lessons.

Did your students enjoy digging around in math in search of patterns? This is a good time to make a list of interesting next steps. Have them make a plot of the digits in the units place of square numbers and other sequences (hint: multiples of numbers under ten). They might enjoy categorising different kinds of sequences, then finding more examples of each. Discovering underlying mathematical patterns can be exciting and satisfying, not only for your students, but also, of course, for you.

Experiment, explore, enjoy!