
How would your students explain?
Students’ explanations of why zero cannot be used in the denominator give educators a reliable measure of their understanding of fractions in general. The perfect time to begin conversations about why putting ZERO in the denominator has no meaning, is when students are first learning about how denominators are created and the roles they play in fractional numbers.
 Mathematicians point out all sorts of reasons why having a denominator of zero will ‘break’ number theory. Most of their arguments are too complex or scholarly for elementary students (and me). However, there are some simple, straightforward explanations which are easily understood by anyone old enough to learn about fractions. In fact, if students are unable to understand why it is impossible to have a denominator of zero, their comprehension of fractions is incomplete.
Mathematicians point out all sorts of reasons why having a denominator of zero will ‘break’ number theory. Most of their arguments are too complex or scholarly for elementary students (and me). However, there are some simple, straightforward explanations which are easily understood by anyone old enough to learn about fractions. In fact, if students are unable to understand why it is impossible to have a denominator of zero, their comprehension of fractions is incomplete.
One way to conceptualize the situation is with a Linguistic Analogy. Another way to think about what would happen is to examine the problem of having a Zero in the Denominator from a Mathematic Point of View. Children might find these thought experiments too abstract. So, the last explanation focuses on Using Concrete Models to demonstrate the nonsense that follows when we try to use a denominator of zero. Before any of the explanations, however, let’s take a close look at What Denominators Do.
What Do Denominators Do?
Many concepts are mixed together to create a student’s understanding of denominator. Which of them are essential?
Ideas which could be included in the definition of denominator:
- Sits under the division bar.
- Names the fraction.
- Called the ‘noemer’ in Dutch.
- One function of a denominator is to count.
- Contains three Latin roots: de – nom – ator.
- Counts the unit fractions needed to fit between consecutive whole numbers.
- Chosen from the set of natural numbers (in elementary math).
- Together with the numerator identifies the fraction’s place on the number line.
- Often mispronounced by young students.
- A concept which expands as students learn higher math.
- And . . .
Which of the many concepts possible, are essential to include in an elementary student’s understanding of denominator? Well, it depends on the student.
If they are multilingual, then translations of the word need to be included in their ‘constellation’ of ideas that define denominator. If they naturally interact with academic subjects through the lens of language, then knowing the Latin roots will be interesting and helpful to them. Gestures and purposeful movement (such as moving from zero to one in four hops on a very long number line, in the hall or with their fingers) should be included. Teachers and parents add the part about how young students often need to practice pronouncing the word in order to get it right.
 From a mathematical view point, students should include the following essentials when defining a denominator.
From a mathematical view point, students should include the following essentials when defining a denominator.
A denominator:
- Names the fraction.
- Sits under the division bar.
- Counts the unit fractions needed to fit between consecutive whole numbers.
- Is the divisor in the division problem.
- In a whole number, the denominator is one.
- Together with the numerator identifies the fraction’s place on the number line.
So, which of the basic understandings tells students that having a denominator of zero makes no sense? This idea is built into the word ‘counts’ as in: A denominator counts the unit fractions needed to fit between consecutive whole numbers. In other words, as far as elementary students are concerned, a denominator must be chosen from the counting numbers.
A Linguistic Analogy
Math is a language such as English, Spanish, Chinese, or Latin. Languages have rules that guide how symbols (that represent ideas) can be used. When readers see an English sentence such as, “I poured coffee into a ___ ,” we expect the blank to be filled with a noun. Using different nouns will create different mental images. English readers will be able to comprehend the sentence even if an unusual noun is used to create a silly image.
I poured coffee into a –
- mug with milk.
- a very large goat with yellow eyes.
- swimming pool.
If a word is chosen from another category – preposition, adverb, article, or ? – English readers will have a difficult time creating a mental image. The resulting sentence will not make sense.
I poured coffee into a –
- yellow and blue
- 17
- quickly
The exact same thing happens in mathematical equations. In order to make sense, symbols must be used in the correct place in the number sentence. When mathematicians, teachers or students see an equation such as, “4×3=__” we expect the blank to be filled with a counting number. Using different natural numbers will create sentences that are either true or false.
4 x 3 =
- 12
- 72
- 43
If a symbol is chosen from a different set, the sentence won’t even begin to make sense.
4×3=
- +
- 1/2
- squid.
Zero in the Denominator from a Mathematic Point of View
Denominators indicate how many equal pieces combine to make one complete object. Zero pieces can’t combine to make anything!
A zero in the numerator means we don’t have any fractional pieces of the size indicated.
A zero in the denominator means that zero pieces are needed to make one whole thing. That’s like saying that 0=1.

AND
Denominators indicate the number of equal pieces which (must be present in order to) make one whole. However, zero describes the absence of pieces. Naming a fraction can only happen when there is a fraction to name. Zero shares a different type of information than the other digits; zero indicates that there aren’t any parts needed to make one whole; that no fraction is extant.
So, LITERALLY there is no fraction with zero in the denominator; zero in the denominator means there IS NO FRACTION. The exact meaning of putting a zero under the division bar is that there isn’t any fraction. There isn’t a number in need of a denominator.
ALSO
These statements make sense in math:

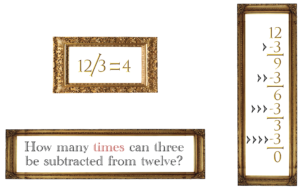
These statements do not make sense in math:
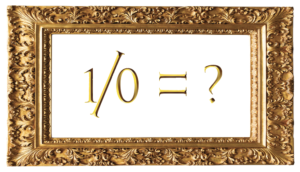

ZERO in the Denominator is as Silly as One over Squid
 Yes, zero is a number, but its function is sometimes different than that of other numbers.
Yes, zero is a number, but its function is sometimes different than that of other numbers.
Placing a zero in the denominator is as illogical as it would be to use a pillow, a great dane, or a daisy. None of them share the type of information that is required. Zero is an arithmetic concept which exists to represent objects which are not present. Zero is not a counting number. When counting objects we automatically start with ‘one’ and move on from there.
There is a reason the set of ‘whole numbers’ is different than the set of ‘natural numbers’. Natural numbers are used for counting, so negative numbers and zero are excluded from that set. Denominators count the number of equal pieces needed to make one whole thing. Counting is included in the definition of denominator. Counting contributes to the constellation of ideas that describe the essential nature of a denominator.
Using Concrete Models
Young children are not ready to explain such an abstract concept as why zero cannot be used as a denominator. They rely on making generalizations based on experience. Which is why students need tons of experience with concrete models of fractions. They can only explain why it’s goofy to have a zero in the denominator using concrete examples or using the number line.

We can’t make a dollar unless we know how many pennies are needed. Denominators tell us how many pennies are needed to make a dollar. So, trying to put zero in the denominator gives confusing information; it would be like saying a dollar is made up of zero pennies. Again $1=0. But that’s not true. It doesn’t make sense. Even if we don’t have any pennies, we still know that 100 of them are needed to make a dollar.
Here’s an example of a possible explanation based on a concrete model using a circle: Denominators show the number of pieces that are needed to make one circle. The smallest number that can be used is one because that is the smallest number needed to make an entire circle. Zero pieces can’t make any circle – so zero can’t be used in the denominator.
If you are trying to make a circle and you don’t have any pieces, then use ZERO in the numerator to share that information. The numerator shows how many pieces there are, whereas the denominator tells us how many pieces are needed to make one whole.
Questions to Get Students Thinking
What is the smallest number that can be in the denominator?
One. When sharing an apple with other people the denominator tells how many people are sharing the apple. One in the denominator means that you aren’t sharing with anyone else, you have the whole apple for yourself.
When you look at a model of a fraction, how can you tell what number is in the denominator?
The number of equal pieces that fit between zero and one
(or make one whole thing) is the number in the denominator.
What does the denominator tell us?
It tells how many unit fractions are needed to make one whole.
What does it mean when you see a zero in the numerator?
The numerator tells how many unit fractions are in the number.
If there are zero unit fractions then we don’t have any of
the type of items that the fractions are talking about.
Would it make sense to have a zero in the denominator? How come?
NO! The denominator tells how many unit fractions make up one whole thing – zero unit fractions can’t make anything! Squid! It doesn’t have any meaning. It means someone made a mistake! It’s silly! You can’t use zero in the denominator!!
How could you use these materials
(the concrete materials they are using at the moment)
to model a fraction with zero in the denominator?
I can’t! There is no fraction to model with zero in the denominator!

Share This Story, Choose Your Platform!
Download Colorful Collections:
A Mindful Exploration of Proper Fractions
Help your students make sense of fractions.
I started teaching in 1987, which means I’ve collected many tips and tricks along the way. In this ebook, I share concepts, strategies, and classroom materials to help you make math sticky.
Along with this useful ebook, you will receive weekly emails from StickyMath@UnCommon-Core.com. I send information like: teacher tips, educational ideas, book reviews, curated lists, reviews of educational sites, and free first drafts of products that I’m creating for my TPT store. That way, you get helpful ideas and free stuff, while I get some feedback before I finalize products and put them up for sale.
I value your privacy. I will never sell your information. You may unsubscribe at any time.
All the best!
Isabelle
Isabelle Hoag M. Ed.


