
Finding the Number of Combinations is Multiplication
Skip counting and repeated addition are fantastic ways to introduce multiplication. However, these models don’t give students the entire picture. Neither skip counting nor repeated addition will help learners understand multiplying fractions. This is one of the reasons that teachers are always looking for more ways to offer students experience with multiplication. Once learners understand the basic idea of multiplication, they need various types of concrete examples to give them practice and additional understanding.
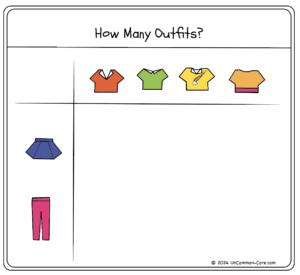
Calculating the total number of combinations in a specific situation is an engaging way to provide learners with another model of multiplication beyond repeated addition. Mixing items of clothing to find unique outfits isn’t the first activity that comes to mind when thinking of multiplication. However, this way of thinking shows students that multiplication can be viewed as identifying intersections, areas of overlap, or interaction between sets of items.
Introducing combinations as multiplication problems can be tricky. Most students will understand the set up of a grid such as the one shown. It should remind them of the multiplication table. However, when the question is posed as a word problem and set up differently, students will need time and practice making sense of what to do.

Initial problems are simple enough that students can find the correct answer by doodling, counting, or even setting up a grid system like the one above. They may not even recognize this as a multiplication problem at first.
Teachers can help students connect finding the total number of combinations with multiplication by inviting them to organize the data in formats that are normally used with multiplication. In addition to the grid or multiplication chart layout, learners who are taught to combine the data into groups of equal size, or to think deeply about the question being asked in the word problem will be able to connect counting all possible combinations with multiplication.
Students will need loads of practice with mixing clothing to make outfits, or whichever concrete model is being used, in order to be familiar with the activity. After they are comfortable matching clothes, they will be able to move on and explore all kinds of items and/or characteristics that might intersect with each other.
Start Simple, Move Slowly
Using multiplication to find the total number of combinations is an  abstract idea. It will take children a while to make sense of what is going on even with several concrete examples. Teachers can make the activities easier for students by choosing multiplication facts that are so simple, they should be self-evident to everyone in the room.
abstract idea. It will take children a while to make sense of what is going on even with several concrete examples. Teachers can make the activities easier for students by choosing multiplication facts that are so simple, they should be self-evident to everyone in the room.
Mixing two T-shirts with one pair of pants is about as simple as a multiplication problem can get. Still, make sure to take time talking through the question and solution thoroughly. After all, students aren’t learning one times two is two, they are learning how to make sense of finding the total number of ways the T-shirts and pants can be worn.
Learners can draw lines to connect each piece of clothing. In this technique, each line represents one complete outfit. Thus, the total number of lines will represent the total number of combinations possible between the T-shirts and pants. For many, this technique will take them through several examples. The lines clearly connect each pair. Counting lines is a simple way to find the total number of combinations. Drawing lines between items is a novel way to find the answer to a multiplication problem. This helps students remember that they are learning a new and different type of multiplication.
However, this technique does not require students to grasp the idea of finding every single outfit that can be created from a given set of T-shirts and pants. Also, as the numbers increase, it isn’t that practical or accurate.

Help students identify the number words and create a multiplication sentence to describe the situation. Encourage them to think about how to write a number sentence that makes sense and will consistently yield the correct answer.

Showing the problem in a grid format allows students to draw pictures of each outfit. Some may want to count the pieces of clothing individually. Talk about the importance of counting complete outfits consisting of a T-shirt and pants.
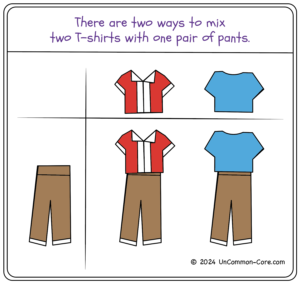
Since children have experience creating outfits by combining tops and bottoms, this example will be familiar to them. This familiarity will help them understand what is going on and help them find words to describe the situation.
Use Layouts that Students Connect with Multiplication
Skip counting and repeated addition are friendly formats identified with multiplication. Another format that screams, ‘multiplication’ is arranging data into equal size groups. Make sure to draw learner’s attention to the structure of each group. Ask them to identify the criteria by which the outfits were grouped. Observe them count the outfits in each group (not the individual items of clothing). Listen to them talk about the groups informally. Have them describe how the groups were created to the class or small group. 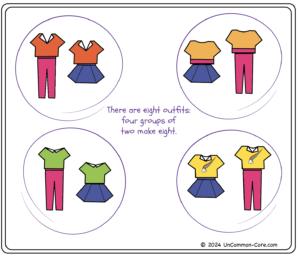
For example, the format above was created so that all outfits with matching tops were included in the same group. Invite students to compare the groups above with their completed combination chart as shown below. 
Students should see that the groups include all the outfits in each column. Since there are four columns – one under each of the four unique shirts – there are also four groups.
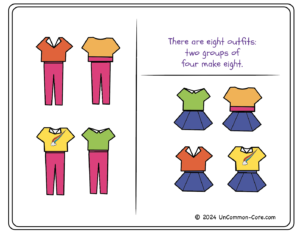
Similarly, when students compare the layout showing two groups of four, make sure they can identify the criteria by which the two groups were formed. Have them tell you that one group contains all the outfits made with the four different shirts and the pink pants, while the other group has every outfit made by combining the shirts with the blue skirt.

Stress the importance of making sure each outfit is counted, AND each outfit is only counted once.
Thank you for reading this far!! Please let me know what you think about using combinations to model multiplication.
Isabelle
Share This Story, Choose Your Platform!
Download Colorful Collections:
A Mindful Exploration of Proper Fractions
Help your students make sense of fractions.
I started teaching in 1987, which means I’ve collected many tips and tricks along the way. In this ebook, I share concepts, strategies, and classroom materials to help you make math sticky.
Along with this useful ebook, you will receive weekly emails from StickyMath@UnCommon-Core.com. I send information like: teacher tips, educational ideas, book reviews, curated lists, reviews of educational sites, and free first drafts of products that I’m creating for my TPT store. That way, you get helpful ideas and free stuff, while I get some feedback before I finalize products and put them up for sale.
I value your privacy. I will never sell your information. You may unsubscribe at any time.
All the best!
Isabelle
Isabelle Hoag M. Ed.

