Skip Count to Multiply Fractions with Whole Numbers

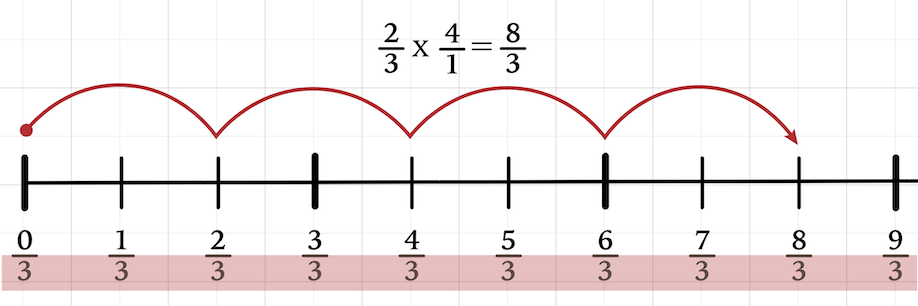
Is it possible to use skip counting to multiply fractions with whole numbers?

Yes! Teach your students how to skip count when multiplying fractions with whole numbers. It’s a great way to introduce multiplication with fractions.

Students already know how to find products by skip counting. So, they will be happy to learn that a similar strategy can be used with fractions. Since skip counting is familiar to your students, it helps them connect what they know with something new. Students who understand the process of skip counting whole numbers will be able to spot the differences quickly. They will notice: the magnitude of the product in relation to the factors is different when fractions are involved, the variations in the number line being used, and the role of numerators and denominators when multiplying fractions.

Take a look at what skip counting looks like when multiplying a fraction with a whole number.

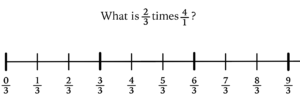
First, students will notice is that the whole number in the problem is written with a denominator of one. If your students can’t explain why whole numbers have denominators of one, take the time to review. Learners should at least be able to describe the denominator as the number of equal hops, or pieces, between zero and one.

Next, students will notice that the number line is written in thirds. Explain that because two-thirds is the fraction in the equation, the number line has to be in thirds, too.

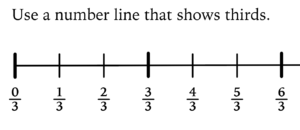
Make sure your students are comfortable with the format of the number line. Take some time to identify the locations of proper fractions, whole numbers, and improper fractions.  Invite your class to do some choral counting starting with zero-thirds, one-third, two-thirds, and so on. These activities will help every student orient themselves to a number line gradated in fractions rather than whole numbers.

Let students know that the product will be written in thirds because the only fraction in the equation is expressed in thirds. For this reason, they don’t have to calculate a new denominator when multiplying a fraction and a whole number. Writing the number line in thirds ‘takes care of’ the denominator.

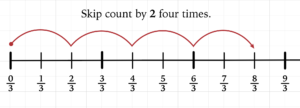
Now, bring their attention to the numerators of both factors. Guide them to see that the basic question is two times four. They should be able to explain how to find the product of 2 x 4 by skip counting.

Start at zero. Skip count by two 4 times.

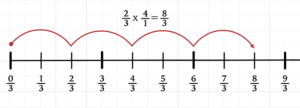
Students already know that the product will be written with a denominator of three. The process isn’t that difficult. However, you want to make sure they understand when and how this works:

• Use this method only when multiplying a whole number by a fraction.
• Mark the number line with fractions that have the same denominator as the fraction in the problem.
• Recognize that the denominator of the factor will also be the denominator of the product.
• Skip count as usual to find the numerator of the product.
• Reduce to simplest form as needed.

Allow plenty of time for questions and class discussion.

For example, consider creating small groups to make posters showing the size of each jump, the size of a whole number, how skip counting compares to the method taught in their text book and so on.

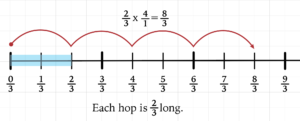
Alternatively, invite your class to write sentences about what they know to be true. “Each jump is two-thirds long,”  “The number line is measured in thirds,” or “The simplest form of eight-thirds is two and two-thirds.” You might want to make this activity into a game of Two Facts and a Fake.

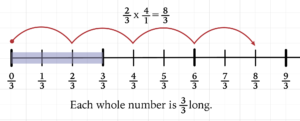
In any case, walk through a couple of examples with everyone to make sure your students are able to use skip counting to find the product of a fraction and a whole number. This method will not replace multiplying numerators and denominators, however it provides students with a familiar format to clarify what is going on. Additionally, it serves as an easy way to check their work.

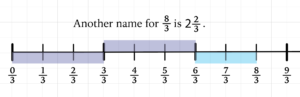
Using a number line can make simplifying the answer much easier, too. As long as students understand how to identify whole numbers on a number line gradated with fractions, they will easily be able to rewrite an improper fraction as a mixed number if needed.

Eventually, using skip counting to find the product when multiplying a fraction with a whole number can be referenced when needed. It could be used to clarify what is happening, check an answer, or find the simplest form of a product.