Take the Mystery out of Equivalent Fractions

Rational Numbers Are About Relationships

Take some of the mystery out of equivalent fractions by inviting students to investigate how equivalent fractions are made before trying to reduce them to their simplest form, or prove their equivalence. Rational numbers are challenging for students to understand. For one thing, there is a never-ending supply of equivalent fractions that share a place on the number line. Understanding that equivalent fractions represent the same number is one of the conceptual puzzles students must piece together in order to work with fractions.

At the same time as investigating how equivalent fractions are created, invite your students to model fractions of all types including equivalent fractions.

Show Students How Equivalent Fractions are Made

The multiplicative identity property of one says that a number’s identity does not change when that number is multiplied by one. This is why multiplying by fractions equivalent to one doesn’t change a number.

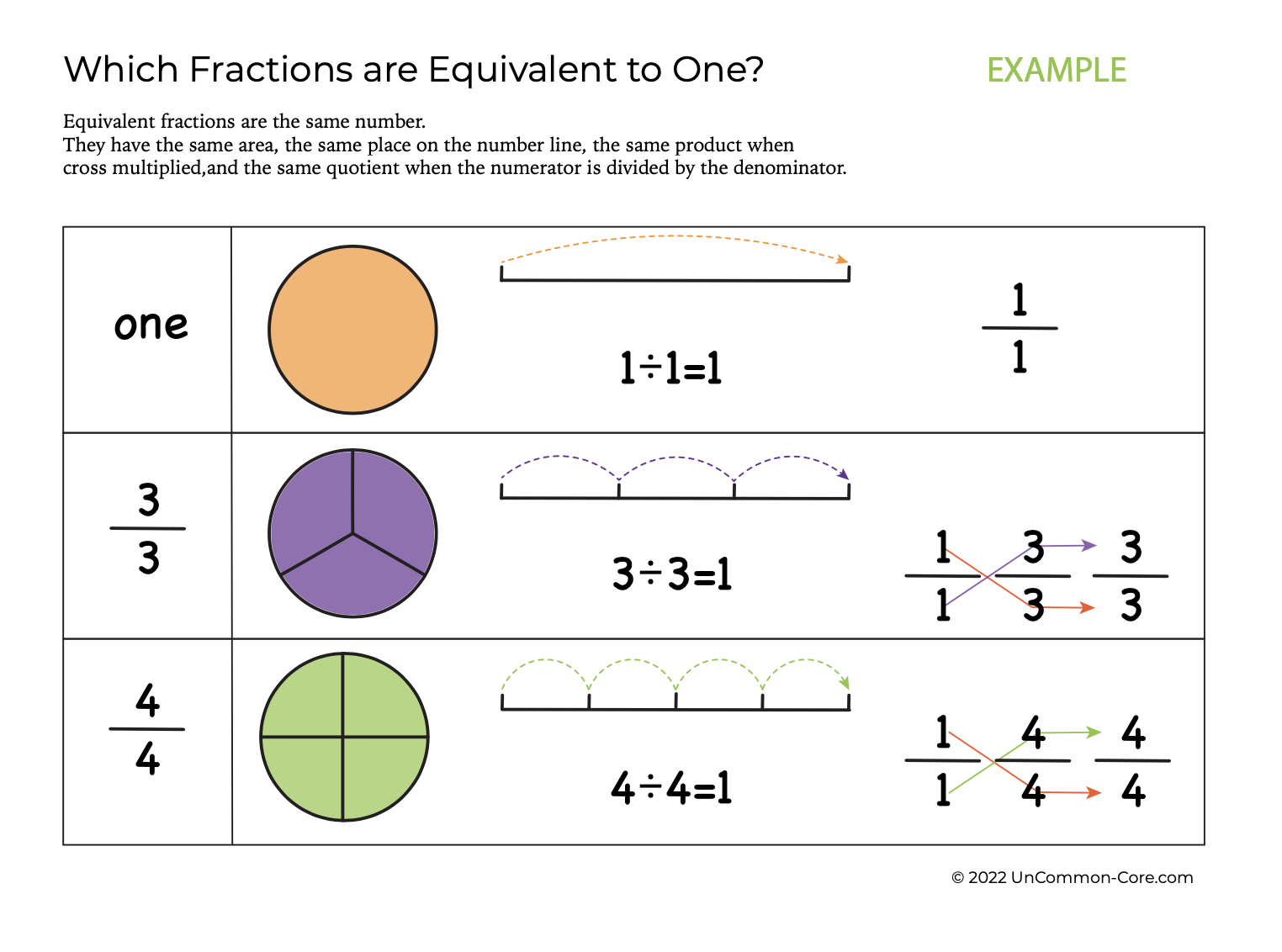
Equivalent fractions:

• reduce to the same simplest form,
• have the same quotient when divided,
• occupy the same place on the number line,
• represent the same proportion,
• share a product when cross multiplied,
• can cause problems for elementary students,
• and their teachers!

Model Equivalent Fractions Often

Have your students model fractions that are equivalent to each other in many different ways. They can see how the models confirm that the fractions are equivalent. After that, they can use the models to determine equivalency.

Once students can accurately show fractions using various models including mathematical notation, they are ready to move on.

Start slowly by asking your students to compare two proper fractions. Gradually increase the difficulty of the task after they are familiar with using models to assess the equality of fractions. The examples shown below are complex and represent responses possible after students have had a great deal of thoughtful experience modeling equivalent fractions.

Students with experience modeling equivalent fractions know that they have to use the same whole thing. When using the number line, the length between zero and one has to be the same. When using an area model, the area of one whole shape has to be the same. After all, a quarter of an hour is longer than half a minute ~ but that doesn’t mean a quarter is bigger than a half!

Encourage your students to find many different ways to describe the numerical relationships in English. Eventually, they may skip this step, however when just starting out, it is important for young students to be able to describe how the two fractions are identical. Since fractions represent portions of a whole, any two fractional numbers that show the same portion of the same whole are the same number.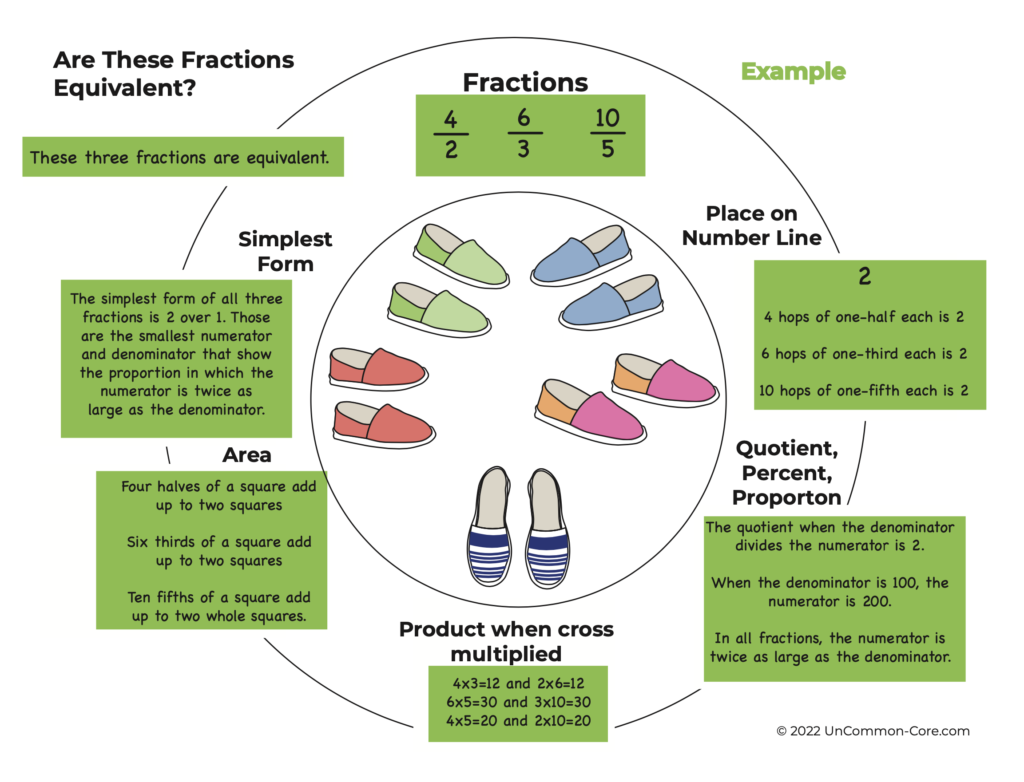

Young students who are just learning equivalent fractions are not ready to understand percents yet. However, if you want to provide your students with a sneak peek of percents, just explain that “percent” meaning ‘for every hundred’ is the name given to a special equivalent fraction. When the equivalent fraction has a denominator of 100, it is called a percent. This will open the door to showing your students how to calculate the value of the numerator when the denominator has to be 100. Dollars, dimes, and pennies make wonderful concrete examples.

Showing that quotients are the same in equivalent fractions is going to be easier when using improper fractions. When using the activities in A Fresh Look at Equivalent Fractions with students in your class, you can tailor the activity to include requirements that you know your students understand well or need to work on.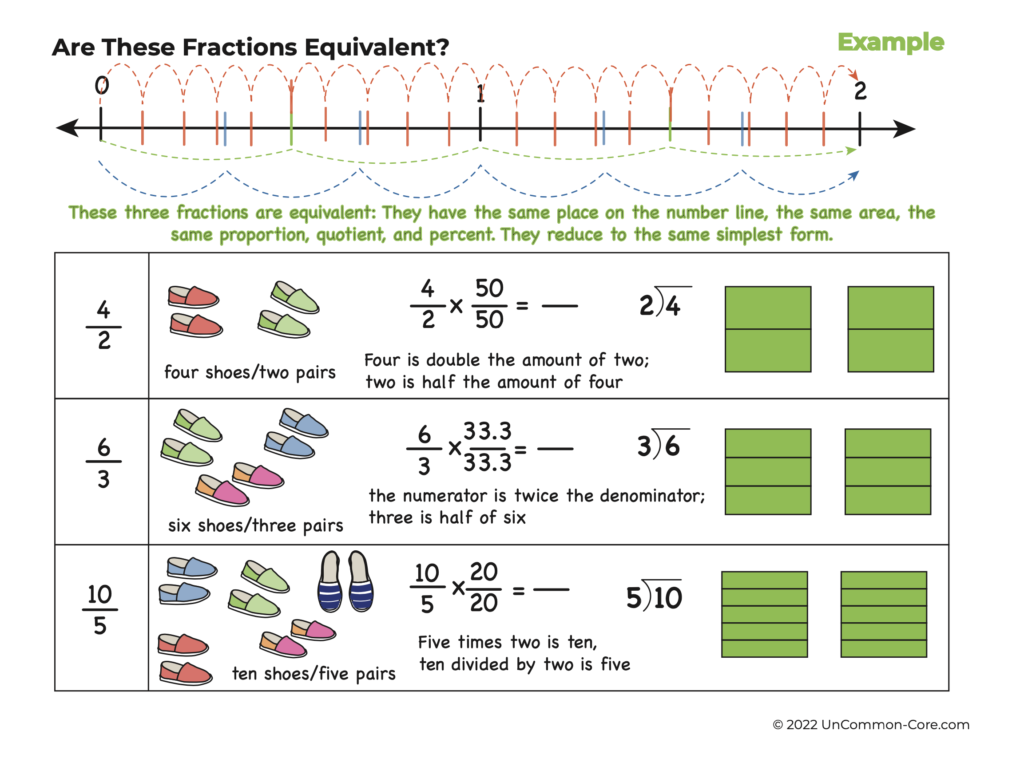

Ask students questions that will get them thinking about the important characteristics of equivalent fractions. Can an improper fraction be equivalent to a proper fraction? How can whole numbers be equivalent to fractional numbers? Are these fractions also equivalent in Spanish or other World Languages?

Check out A Fresh Look at Equivalent Fractions.