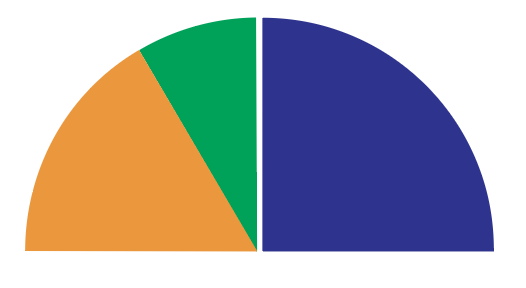
Use Manipulatives to Find Least Common Denominator
YES! You can use those colorful plastic fraction pieces to find the LCD when adding fractions that do not have the same denominator. Under special circumstances, the least common denominator for a pair of numbers is the difference between unit fractions that have those numbers as denominators.
That’s right! The difference between one-half and one-third is one-sixth which is also the LCD of 1/2 and 1/3 and the LCM of 2 and 3.
How Does this Work?
Let’s say we want to add ¾ and ⅚.

The first thing we need to do is find a common denominator. We could multiply, however since both the GCF and the difference between four and six is two, we can use fraction manipulatives to find their least common denominator.
Select pieces that represent a unit fraction for each denominator.

Place the small piece on top of the larger piece.

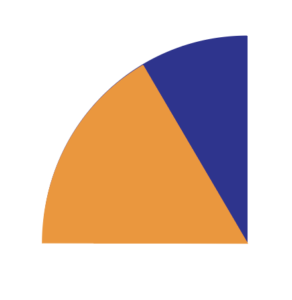
Use the ‘Goldilocks’ method to find a unit fraction that exactly fills the space between them.
Gather some likely candidates.

Look for one that is not too big,
 not too small,
not too small,
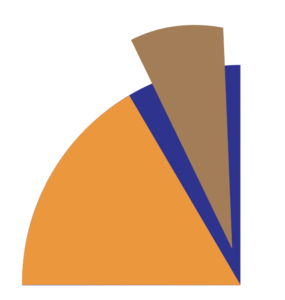
but just right!
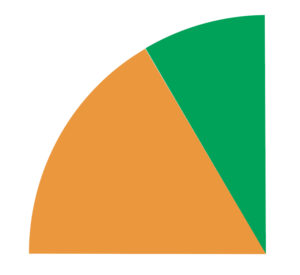
Wow! The green unit fraction together with the 1/6 piece have the same area as the 1/4 piece.
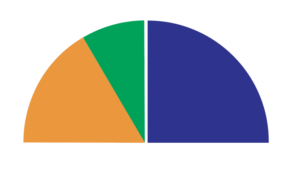
What size is the piece that fits perfectly?

The name of the fraction is based on how many unit fractions of that size are needed to make one whole number. In this case, there is a twelve in the denominator.
So, 1/12 +1/6= 1/4. To put it another way, 1/12 + 2/12= 3/12. Which also means that when adding fractions with 4 and 6 in the denominators, the difference between their unit fractions is equal to the least common denominator LCD.
Four and six are part of a unique group of number pairs that have this relationship. Most of the time, LCD cannot be calculated this way.
Using Manipultavies to Add Fractions with Unlike Denominators
Now, the students can use their manipulatives to find equivalent fractions for three-fourths and five-sixths that have a denominator of twelve. Encourage your students to keep notes and doodles to show the step by step progress. Challenge them to look for numerical relationships as they find equivalent fractions.
In order to represent 4/6 in twelfths, find out how many twelfths are needed to cover the same area as four-sixths.

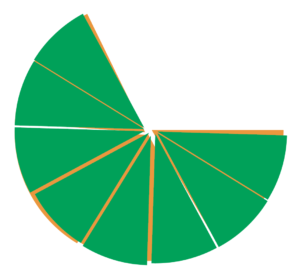
Then find out how many twelfths are needed to cover the same area as three-fourths.

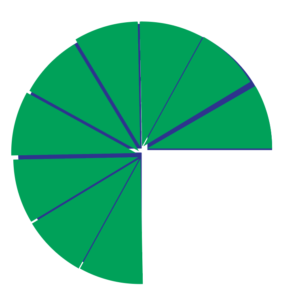
This leaves the students with 8/12 and 9/12 to add together.

First, they can use some of the twelfths to make one entire circle.
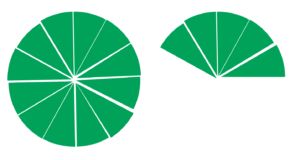
Which leaves them with an answer of one and five-twelfths.
 This way of solving addition problems is not quick. It is not efficient. It does provide a concrete model for each step in the process of adding fractions with unlike denominators. This method only works when you use numbers with carefully selected denominators.
This way of solving addition problems is not quick. It is not efficient. It does provide a concrete model for each step in the process of adding fractions with unlike denominators. This method only works when you use numbers with carefully selected denominators.
After a couple of days of this, imagine how happy your students will be when you tell them there is a faster way to add fractions with unlike denominators! A way that only uses numbers and math symbols! Yippie!
Until then~
Which Pairs of Unit Fractions can be used with this Method?
The number pairs in which their GCF is the difference between them that are also likely to be represented in fraction manipulatives are:
(2,3) (2,4) (3, 4) (3, 6) (4,5) (4, 6) (4, 8) (5,10) (6,8) (6,12)
You can use these pairs of numbers in the denominator of addition or subtraction problems and use the method shown above to find their least common denominator LCD.
Fractions are notoriously difficult to conceptualize and work with ~ making math class one of the most dreaded hours of the school day for many young students.
This special group of numbers ~ a subset of a general principle connecting GCF and LCM ~ gives you a concrete way to help your students visualize what is happening when adding fractions that do not have like denominators before introducing prime factors.
Share This Story, Choose Your Platform!
Download Colorful Collections:
A Mindful Exploration of Proper Fractions
Help your students make sense of fractions.
I started teaching in 1987, which means I’ve collected many tips and tricks along the way. In this ebook, I share concepts, strategies, and classroom materials to help you make math sticky.
Along with this useful ebook, you will receive weekly emails from StickyMath@UnCommon-Core.com. I send information like: teacher tips, educational ideas, book reviews, curated lists, reviews of educational sites, and free first drafts of products that I’m creating for my TPT store. That way, you get helpful ideas and free stuff, while I get some feedback before I finalize products and put them up for sale.
I value your privacy. I will never sell your information. You may unsubscribe at any time.
All the best!
Isabelle
Isabelle Hoag M. Ed.

