Modeling Fractions

The More; the Better When it Comes to Modeling Fractions

 Students need to experience several types of models and manipulatives in order to generalize concepts about fractions.

Like any number, fractions have a place on the number line, which is why they are an essential linear model. But number lines alone aren’t enough for students to build intuition and a complete understanding of fractions. Listed below are some of the various ways to model fractions: linear, area, set, duration, linguistic, angular, and symbolic.   Volumetric models are discussed on a different page.

First students learn to model fractions; then students model fractions to learn.

There is no end to the number of ways to model fractions. I included creative ideas that use manipulatives that you may already have in your classroom or are easy to come by. I’ve also included simple activities that could be used with those manipulates under each list.

Linear Models

• yarn
• rulers
• string
• ribbons
• yardsticks
• tape measures
• edges of shapes
• Cuisenaire Rods

Measure People to model fractions

Set up stations where students can measure the lengths of feet, stride/pace, shoulder width, hands*, and cubits*. Consider inviting specialist teachers and administration so students can measure adults.

Compare adult and student sizes. Let each student use one of their measurements as the numerator and the corresponding adult measurement as the denominator. Chart or display the results. Is

*Let your students research these ancient measurements first. Cubits have long been used in building ancient structures, whereas we still use ‘hands’ to measure horses to this day.

Measure the Room to model fractions

Give teams of students a clip board and a measuring tape. Let them measure and record the height and width of straight lines in the room: door jams, wall tiles, floor tiles, desks, chairs, windows, books. Give teams different units of measurement so that half of your students measure the objects in centimeters and the other half measure in inches.

Pair students so that each pair measured the same object with different units. Then have the pairs make fractions out of the measurements for each object. Use the measurements made in larger units as the numerator (or the other way around, as long as everyone does it the same way!) and find the quotient for each object measured. For example, pair a student who measured in centimeters with a student who measured in inches. Each of them measured the length of a desk. The desk measured 25 inches and it also measured 64 centimeters. The quotient is about .4. Have the pair find the quotient for other items they measured.

Compare the results of the entire class and discuss. How come, regardless of the item measured, the quotient (and thus the relationship between cm and inches) was the same?

Area Models

• grid paper
• unit squares
• tangrams
• origami paper
• pattern blocks
• one shape tessellations

Model with Shadows

Give teams of students chalk, a clip board, rulers, cardboard squares, and some objects like balls, books. Take them outside on a sunny day. Let them trace and measure the shadows of each object. They can make a grid with the cardboard square, rulers, and chalk.

Give teams different units of measurement and different shadows to measure. Let half of your students measure in square inches and the other half measure in centimeters. Back in the class room pair up students who measured the same items using different units. Have them put the

Use Origami paper to model equivalent fractions:

Give small groups of students pieces of origami paper. Show them how to fold the paper so that each resulting shape is equal to the others. Then have them fold one square in halves and another in fourths or eighths. Have them color in one-half on all the folded sheets. Let them make a mini poster to show that when starting with the same amount of space (same area), one-half of that area takes up the same amount of space as two-fourths or one-eighth.

Set Models

• buttons
• origami animals
• bottle tops
• paper clips
• pebbles
• centimeter cubes
• dry beans
• novelty toys

mini erasers

Unit Fractions of Office Supplies

Give each team a boxed set of office supplies ~ 144 paperclips, 24 crayons, 12 markers, six pack of tape, or a box of batteries. Alternatively, print and share ads for boxes of office supplies.

Let the groups use a calculator if needed. Have them record how many items in half a box, a third of a box and so on.

Unit Fractions of a Dozen

Give each group a collection of a dozen items. Let them record how many items are in half of a dozen, thirds, fourths, and so on.

Durational Models

• clocks
• digital timers
• sand timers
• stop watch
• windup toys or
• pull back racers
• music
• rhythm
• timing activities
• jump ropes
• heart beats
• seasons of the year

Sand Timers

Give teams of students a set of sand timers and paper to record their results. If needed tape over the decimal marking and write the fractions on each timer.

Let each team record the number of flips needed in order to measure a minute. Make sure they count the first flip! Do three or four trials for each sand timer. How many times is the 1/2 minute timer flipped in one minute? Compare that with the number of times the one minute timer is flipped.

How Many Centimeters in a Minute? Wait – what?

Gather the class to take notes on some unusual races. Set yardsticks on the floor next to the ‘race track’. Appoint someone to time the race. Wind up or pull back some cute toys and cheer quietly as they move along the track. Measure how far each toy went in one minute and express that information as a fraction.

Linguistic Models

• everyday language
• story problems
• asking questions
• second languages
• vocabulary lists
• dictionaries
• glossaries
• math journals
• class discussions
• writing about math

Student Authors

Invite each student to write a story problem about a given equation. Let them create a colorful display of several different ways to model the story problem. If you are lucky enough to have multilingual students, ask them for literal translations to demonstrate how languages other than English talk about fractions.

Share and compare the diverse results considering that everyone had the same starting point.

Vocabulary IS Content

Listen to your students discuss division, whole numbers, and unit fractions.

Do they own the essential academic vocabulary? Listen to their questions~ their peer to peer conversations. Read their reflections and explanations.

Have they ‘just met’ each word or are they good friends?

Angular Models

• degrees
• protractor
• angles
• square corners
• straight lines
• fractions of circles sets
• stencils
• compass

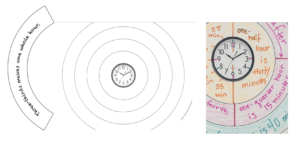
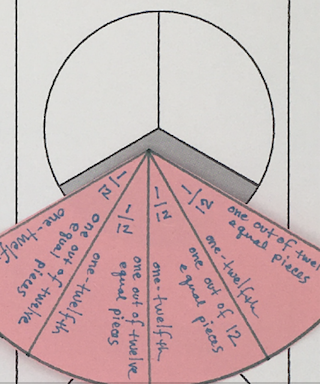
Young students can easily tell when a circle is complete or whole. This is one reason that fractions of circles are a fantastic starting point for introducing rational numbers.

Angular models measure distance around the circle’s center. This also corresponds to fractions of the circle’s area.

When your students are ready to measure angles, then you can separate angular models from area models. Until then, it makes sense to consider them area fractions.

Graphic Models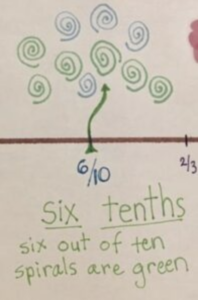

• doodles
• images
• pictures
• cartoons
• diagrams
• blue prints
• maps
• create an illustrated number line as a class

Doodles

Encourage students to make quick abstract doodles to help them ‘think on paper’ while dividing whole numbers by unit fractions.

Perhaps they could show the whole numbers with rectangles and then mark off 5 segments to show fifths. Doodles are not accurate or to scale, they simply show basic information.

Concrete to Abstract

Give simple story problems to teams. Have them make three illustrations of their story problem ~ one precise with lots of detail, one like a quick sketch of the information, and the last like an abstract design. All three illustrations should contain enough information to solve the problem.

For example, image the doodles that students could create for this story problem: There are 12 marbles and three children. How could the marbles be shared equally? What fraction of those marbles would each child have? The concrete image would show hands holding marbles. The quick sketch could show outlines of hands holding outlines of marbles. The abstract image could show three circles with four smaller circles inside each of them.

Display the graphics with the story problems and the solutions.

Symbolic Models

• Mathematical Notation
• Math text
• base 10 number system
• Roman, Egyptian or Babylonian number systems

Eventually, students will be expected to understand mathematical notation fluently. The ultimate goal is for students to use mathematical notation to model and solve math problems.

Fluency includes being able to translate equations from mathematical symbols into a variety of models, and back into mathematical notation accurately.

This will make it possible for advanced students to translate displays of data into equations and math text, or to create data displays based on math texts or mathematical notations.

Have your students explain their thinking. Encourage them to revise their thoughts when new information becomes available. As your students progress, continue to collect their questions, comments, and observations about fractional numbers.