
What is the Big Deal with Rational Numbers?
 Understanding fractions is essential in order to participate in today’s society, comprehend the news, make informed decisions, be savvy when purchasing big ticket items, or even just follow a recipe. Learning about fractions requires students to rethink everything they already know about how numbers work. Students must take in loads of new ideas and expand their knowledge of basic arithmetic such as, ‘in multiplication, the product will always be larger than either factor.’
Understanding fractions is essential in order to participate in today’s society, comprehend the news, make informed decisions, be savvy when purchasing big ticket items, or even just follow a recipe. Learning about fractions requires students to rethink everything they already know about how numbers work. Students must take in loads of new ideas and expand their knowledge of basic arithmetic such as, ‘in multiplication, the product will always be larger than either factor.’
In order to become proficient in using fractions, students must completely grasp novel concepts and vocabulary such as numerators, denominators, factors, equivalence, simplest form, or lowest terms, and how each of these concepts impact addition, subtraction, multiplication, or division. Students need to expand their number sense to include
relationships such as reciprocals, & ‘when the denominator gets larger, the piece of the pie gets smaller,’ or ‘the denominator shows how many equal pieces are needed to make one.’
In addition to whole – part relationships, fractions can have many uses which take time for students to explore. They are used to weigh & measure, to show a division problem, or to indicate ratios. Simply understanding that a fraction is one number and not two different numbers written one on top of the other can be challenging at first. There is so much new information that students are likely to get overwhelmed unless they are given lots of processing time. Teachers need to pace lessons in order to make sure their students are able to make sense of each new idea before they have to grapple with the next one.
Teaching Fractions: Seven Ideas that Work
 What can you do in your class to support your students’ understanding of fractions & rational numbers Comprehending fractions, decimals, & rational numbers, plus knowing how to use them accurately when making calculations is important. Learning about fractions is arguably one of the most challenging academic topics facing the students in your math class this year. You are committed to helping them achieve their best, so now what?
What can you do in your class to support your students’ understanding of fractions & rational numbers Comprehending fractions, decimals, & rational numbers, plus knowing how to use them accurately when making calculations is important. Learning about fractions is arguably one of the most challenging academic topics facing the students in your math class this year. You are committed to helping them achieve their best, so now what?
Have Confidence in Your Own Math Skills
Start with your own understanding. Can you write a story problem that requires dividing by a fraction? Multiplying by a fraction? Even if you don’t teach these specific skills, your teaching will be more informed if you are up to date on all concepts connected with fractions.
 Many of us believe we know exactly how to teach fractions. However, there are so many facets to understand and investigate that dividing up a couple of pizzas just isn’t going to cut it (sorry). Chances are we teach fractions the same way we were taught. Usually, this is only a small part of the story (dare I say a fraction of the whole idea? No? Ok forget it).
Many of us believe we know exactly how to teach fractions. However, there are so many facets to understand and investigate that dividing up a couple of pizzas just isn’t going to cut it (sorry). Chances are we teach fractions the same way we were taught. Usually, this is only a small part of the story (dare I say a fraction of the whole idea? No? Ok forget it).
Make sure that you know what you’re supposed to know in order to be the best teacher you can be. If needed, find ways to acquire more expertise with rational numbers. In other words, each of us must make a conscious effort to expand our understanding of rational numbers. Make sure you have a complete understanding of skills and knowledge related to rational numbers.
 Take a moment to assess your own skills related to fractions. Khan Academy has free courses covering fractions, decimals, & percents. A simple review of the big ideas might be all that is needed to give you & your confidence a boost as well as inform your teaching.
Take a moment to assess your own skills related to fractions. Khan Academy has free courses covering fractions, decimals, & percents. A simple review of the big ideas might be all that is needed to give you & your confidence a boost as well as inform your teaching.
Explicitly Compare/Contrast Whole Numbers & Rational Numbers
Can a fraction be even or odd? When you multiply rational numbers will the product always be larger than the factors? How many equivalent fractions are there for one-half?
In some ways, rational numbers work just like integers; they have a specific place on the number line, they can be multiplied by 1 without having to move to a new place on the number line, & their sum will always be larger – or their difference always smaller – than the operands.
 At the same time, there are many ways in which rational numbers differ from whole numbers. These differences, and the reasons behind them, cause problems for students (and for some of us teachers). When multiplying rational numbers between 0 and 1, the product will be less than the factors. In the wild world of fractions, suddenly every number has a denominator. One-half can relate to different amounts; one-half of 100 is not the same amount as one-half of 22.
At the same time, there are many ways in which rational numbers differ from whole numbers. These differences, and the reasons behind them, cause problems for students (and for some of us teachers). When multiplying rational numbers between 0 and 1, the product will be less than the factors. In the wild world of fractions, suddenly every number has a denominator. One-half can relate to different amounts; one-half of 100 is not the same amount as one-half of 22.
Using class time to discuss how integers and rational numbers are different and alike is time well spent. Conversations like this let your students know what is ahead and signal to them how important this work will be. Listening to your students will give you insights into the kinds of problems they may have conceptualising fractions or other rational numbers and help you identify any misconceptions that may need to be addressed. Frequent conversations about math will help you pace lessons to keep students engaged without letting them get overwhelmed.
For example, when unpacking ideas such as what happens to numbers when multiplied by 1, it is important to think about the process from the child’s point of view. Your students may understand that 3 x 1 = 3. Yet this knowledge might not automatically transfer to an equation that looks like this: 3/1 x 18/18 = 54/18ths. Before jumping in with your teacher cape on, take time to collect questions and reactions from your students. Imagine this equation from their point of view. Why does 3 have a denominator and why is that denominator one? Why is 18/18 equal to 1? And where does 54/18ths belong on the number line?
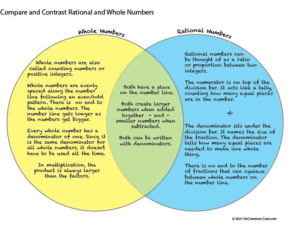
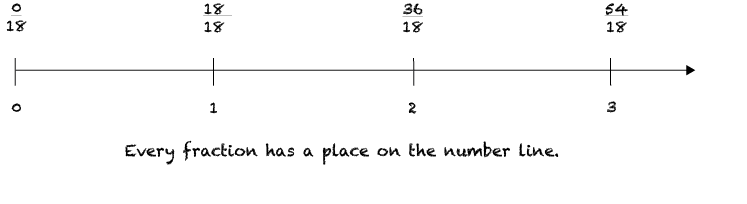 When students begin to calculate with rational numbers, familiar rules governing arithmetic shift. Until your students know which rules and properties stay the same and which have changed, it will be difficult for them to make sense of rational numbers. There are many ways to include a systematic review of concepts that apply to both integers and rational numbers and concepts that don’t. You might invite your students to help you create a giant Venn Diagram to show where the concepts differ and where they overlap.
When students begin to calculate with rational numbers, familiar rules governing arithmetic shift. Until your students know which rules and properties stay the same and which have changed, it will be difficult for them to make sense of rational numbers. There are many ways to include a systematic review of concepts that apply to both integers and rational numbers and concepts that don’t. You might invite your students to help you create a giant Venn Diagram to show where the concepts differ and where they overlap.
 Why not collect and post your students’ questions about rational numbers in order to start thinking about how rational numbers are similar and different from integers. Add some questions or puzzles that anticipate upcoming learning goals. This list could help organise your class exploration of rational numbers. Check off questions as the answers become apparent. Revisit the list of questions as a reflection guide near the end of the year.
Why not collect and post your students’ questions about rational numbers in order to start thinking about how rational numbers are similar and different from integers. Add some questions or puzzles that anticipate upcoming learning goals. This list could help organise your class exploration of rational numbers. Check off questions as the answers become apparent. Revisit the list of questions as a reflection guide near the end of the year.
You may decide to show integers under the class number line and show fractions, decimals, & percents on top. You may even create a special number line showing the segment from zero to one in detail. In any case refer to the number line often to increase your students’ understanding.
Once similarities and differences have been identified, invite your students to create posters reminding the class of specific information they are learning. Encourage them to think of simple explanations and pair them with informative illustrations. Then, refer to the posters – and the conversations that generated them – whenever that topic comes up again.
Continue checking in with your students to gauge how well they are able to make sense of the similarities and differences between integers and fractions in their daily work. Note how easily your students use correct academic vocabulary to express their thoughts about fractions and integers as well as any lingering questions they may have.
Focus on Academic Vocabulary
Any specialized subject has a nomenclature all its own. Artists discuss hue and saturation of colors, historians value primary over secondary sources, and musicians know the difference between major & minor keys, and tempi such as presto or adagio.
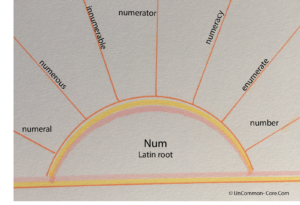
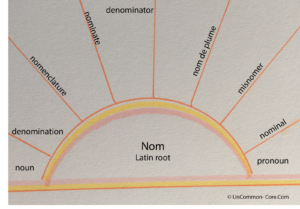
Mathematics is no different. Studying the vocabulary of fractions is important to your students’ success. Knowing, understanding, speaking, and writing with vocabulary words such as numerator, denominator, reciprocal, or ratio is essential for several reasons. First, knowing the jargon helps students feel as if they are a part of the mathematical world which they are studying. Second, vocabulary words help students express specific ideas and ask precise questions. Without being able to use the vocabulary, how can students express their ideas? Vocabulary words act like hooks upon which students can hang the ideas associated with them. Learning the terminology is part of the process of learning about fractions.
In addition to modeling the correct use of academic vocabulary, provide many opportunities for your students to practice pronouncing the words and phrases they need while learning fractions. Introduce math vocabulary during spelling, reading, or word study. If your students are learning Greek or Latin roots, let them investigate the origins of terms like fraction, numerator, and denominator. Give your math students time to write about what they are learning. Consider using nonfiction math related texts when you read aloud to your students. Post displays that use math vocabulary where students can review them often. Refer to the posters frequently, making sure that your students understand the information – and the vocabulary – that is being presented.
Use a Variety of Mathematical Manipulatives; Especially Number Lines
Students require a lot of practice with fraction manipulatives. Using fractions to measure lengths, to express ratios, to identify subsets of a collection of items, or to describe and compare the area of shapes are each unique and important skills. Students of all ages need to explore concepts in a variety of situations, using a variety of manipulatives. This helps them build a flexible understanding of fractions. Plan extra time for students to ‘mess around’ with math manipulatives before using them in academic situations.
Refer to the class number line frequently and often while teaching about fractions and rational numbers. Placing fractions on the number line helps students expand their ideas about numbers and helps them compare & contrast whole numbers with fractions. Ordering fractions or decimals by size is a fundamental skill needed in order to make accurate calculations.
Educational researchers theorise that due to its simplicity and usefulness, each of us carry a ‘mental number line’ with us. Your students are in the process of creating their personal number line. Their mental model is updated every time they learn new information about how numbers work. For example, their mental image of a number line ‘gets longer’ as children discover larger and larger numbers. Learning about rational numbers can shake up the mental images of number lines that children have built up to that point.

Before fractions, students had a mental image of a long thin line with little, evenly spaced, marks along it. There was one integer for each mark along the line. The distance between each mark on the integer number line is exactly the same: ‘one.’ The integers follow a sequential pattern so that each numeral is one whole space larger or smaller than its neighbors. Some students have mental images filled with details and others have more of a ‘big picture’ kind of view. Students can visualize hopping up and down their mental number lines as they add, subtract, multiply, and divide. They know that every other number is even or odd. They know that if they start from zero & move to the
right, every 10th number will have a 0 in the unit’s place.
One reason that fractions are so difficult for students to comprehend is that they do not fit onto the mental image of the number line as they know it. For starters, students often do not know where specific fractions or decimals belong on the number line. Next, rather than imagining a long line of evenly spaced numbers, students can see that fractions

fill the spaces between whole numbers. Fractions snuggle in between each other. There is always room for more. Students who had previously imagined an infinitely long number line with the same amount of distance between each number, must now update that image to include a stretchy, elastic number line with enough space for an infinity of rational numbers between each integer.
Also, fractions do not line up following the even/odd pattern that was so reliable in past versions of their mental number line. There are multiple formats to use when writing rational numbers; proper fractions, improper fractions, mixed numbers, & decimals. Many students struggle to expand their mental image of the number line to include equivalent fractions, decimals, and percents. They need time and experience to construct a more sophisticated understanding of the number line.
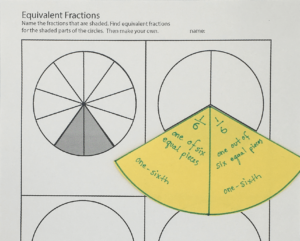 Being able to locate numbers on number lines in class, & eventually on the number line students visualize internally, is an essential step in learning how to compare and order fractions. Once students can locate three-fourths on the number line, they can see that it is smaller than one & larger than one-half. Knowing how big a number is helps students tell if a sum ‘looks right’ or if they might have miscalculated. Knowing the size of a number helps students make estimates and conceptualise how to solve word problems. Being able to locate fractions on the class number line gives students the information they need in order to update their mental models and make sense of rational numbers. Additionally, this type of activity helps students think of fractions as numbers. Older students can use number lines to explore equivalent fractions.
Being able to locate numbers on number lines in class, & eventually on the number line students visualize internally, is an essential step in learning how to compare and order fractions. Once students can locate three-fourths on the number line, they can see that it is smaller than one & larger than one-half. Knowing how big a number is helps students tell if a sum ‘looks right’ or if they might have miscalculated. Knowing the size of a number helps students make estimates and conceptualise how to solve word problems. Being able to locate fractions on the class number line gives students the information they need in order to update their mental models and make sense of rational numbers. Additionally, this type of activity helps students think of fractions as numbers. Older students can use number lines to explore equivalent fractions.
Visualizing fractions as pieces of a circle is a great introduction to understanding fractions as part of a whole. Everyone can tell when the circle is complete, or when a fraction is more or less than half of the way around the circle. Also, circle fraction pieces have the advantage of being able to fit over any circular illustration in textbooks or handouts. Even if the edges of the circle don’t match up, the tip of the fractional pieces will wedge into place allowing students to use manipulatives to help them understand illustrations. Also, pie shaped wedges are easy to stack in order to find equivalents and make comparisons. Consider having your students make their own set of circular fraction. manipulatives as a perfect introduction to whole/part relationships. Help your students make the
connection between an analog clock face and circle fractions.
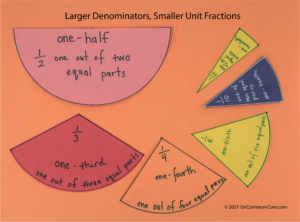
Older students can use circle fraction sets to illustrate and test equivalence. Colorful sets of circle fractions provide a concrete demonstration of equivalent fractions for one. Placing all the like fractions together to make entire circles show that two halves are one, three thirds make one, and so on. Similar processes can be used to find equivalents for ½, ⅓, and other proper fractions.
Linear fraction tiles can also be used to show equivalencies, providing students with another way to visualise the relationship between a whole and its parts. Illustrating whole/part relationships with manipulatives other than circles is important so your students have multiple representations of fractions available to them.
Spend class time exploring the properties of fractions. Have your students collect, organize, and display data to show what happens to the size of the unit fraction as the denominator grows larger. Students might start this project by placing various unit fractions on the numberline. Make sure that all the fractions they use in this exploration are part of the same whole. They should soon notice that unit fractions with larger numbers in the denominator will be closer to zero than unit fractions with smaller numbers in the denominators.
Classrooms are full of things and people to measure. Measuring lengths is an important, hands-on activity that will provide another context in which your students can build their understanding of fractions. It is easy to find materials for students to practice with. Students could measure durations with sand timers, a clock, or stopwatch. They could measure weights with a balance or scales.  Set up a class thermometer by the window & have students take note of the temperature to the nearest half degree. These kinds of activities will help children develop an understanding of what it means to “measure length to the nearest half inch,” or “measure your weight to the nearest quarter pound.” Invite your students to explore ways in which changing the units of measure impacts the accuracy and the magnitude of the answer.
Set up a class thermometer by the window & have students take note of the temperature to the nearest half degree. These kinds of activities will help children develop an understanding of what it means to “measure length to the nearest half inch,” or “measure your weight to the nearest quarter pound.” Invite your students to explore ways in which changing the units of measure impacts the accuracy and the magnitude of the answer.
Another innovative mathematical manipulative is a piece of paper. Using colorful washi and standard instructions in math class can help students explore fractions in an interesting format: folding origami models. Once your students understand how to follow the symbols and directions, you can send the instructions and paper home for them to continue independently.
Imagine what happens when older students fold a square in half, then fold that half in half, then fold that half in half, and so on. First, they will see an example of a geometric series that converges absolutely. Then, at the same time, they will see why the sum of the equation below must be one.
? = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 + 1/1024 + 1/2048 + 1/4096 . . .





Strive to give your students an assortment of thoughtful assignments that use different ways to represent fractions. When students have had lots of experience with a variety of manipulatives they are more likely to be able to find a way to think about fractions that matches the problem they are solving.
Connect Fractions with Other Subjects;
Bring additional academic subjects into your math class. Science, literature, history, and other areas of mathematics; geometry, money, telling time all have important connections to rational numbers. Teachers are becoming more accustomed to integrating literature into our math lessons. There are an increasing number of children’s books written with this in mind such as the Charlesbridge Math Adventures like Pythagoras and the Ratios. Examples of how math is relevant to a variety of subjects are plentiful. Helping students make connections between topics supports their understanding of the complex relationships that make up our world.
Textbooks are full of sentences such as, “ More Americans voted in the 2020 election — two-thirds of the voting eligible population — than in any other in 120 years.” This Washington Post article goes on to compare voter turnout in the past using percentages and providing a concise analysis of the data. In order to help students pull useful, accurate, information from this or similar texts, bring math into your subject area classes.
Look for ways to revisit fractions in various contexts throughout the entire school year. This could happen by providing fraction oriented games for indoor recess or free time, or by bringing your students’ attention to any fractions that show up while studying other topics. Point out how understanding the fractions helps understand the topic as well. Include several fraction related children’s books in your class library. You might want to mark some of the most common fractions around the outside of the analog clock hanging over the classroom door.
Understanding rational numbers is essential in order to understand test scores, calculate grades, and support academic success. Make sure that your students place higher than the ‘top 75 percent’ of their class when it comes to understanding rational numbers.
Invite Colleagues & Families to Lend a Hand
 Involve other teachers and caretakers in the process of teaching fractions. Specialist teachers, interventionists, family, and caretakers have a lot to contribute when it comes to helping your students learn about fractions outside math class. When students realize that the conversation about fractions continues in specialist classes, at home, and in the community, they will be reminded that understanding fractions is important.
Involve other teachers and caretakers in the process of teaching fractions. Specialist teachers, interventionists, family, and caretakers have a lot to contribute when it comes to helping your students learn about fractions outside math class. When students realize that the conversation about fractions continues in specialist classes, at home, and in the community, they will be reminded that understanding fractions is important.
Art teachers may help connect topics such as scale & proportion, recipes for mixing colors, identifying iterative motifs, angles, and design theory related to fractions. Music teachers have many opportunities for bringing in ideas related to fractions, including rhythm, repetition, pitch related to length of strings or amounts of water in glasses, duration of notes depending on the time signature, and scales.
Physical education may be one of the last classes in which students expect to learn about fractions. However, combining math with movement is a very powerful strategy to engage students and provide them with another perspective while exploring fractions. Integrating sports and math is beneficial for all students. Yet for some students, seeing how fractions & decimals are used in sports may be essential in order to spark and maintain their interest.
Shopping, cooking, banking, bedtime stories, and screen time can contribute to a child’s understanding of fractions. Why not send families & caretakers a list of educational cartoons, simple recipes (that require a lot of measuring), or ideas for games that involve practicing fraction skills?
Invite multilingual families to share vocabulary and have conversations about fractions in all their child’s languages. You can offer your students a larger range of activities and multiple venues for learning about fractions when you invite colleagues and families to participate.
Let Students Reflect on Their Work
Plan time and activities that invite students to reflect on what they have learned as well as the quality of their work. Looking back, comparing where they started with where they are now, or simply listing the results of their hard work, gives students perspective and insights into their achievements as well as their goals. This kind of retrospection helps students consolidate their understanding of the subject matter. It gives them a better picture of how they make meaning from academic projects. It allows them to regroup and refocus.
 During the process of considering how much they have learned, unresolved questions or puzzles might pop up. Take note of what kinds of questions remain for your students. Decide if any or all of your students need reteaching or review of specific concepts or skills. Continue until the kinds of questions that remain anticipate next year’s math curriculum.
During the process of considering how much they have learned, unresolved questions or puzzles might pop up. Take note of what kinds of questions remain for your students. Decide if any or all of your students need reteaching or review of specific concepts or skills. Continue until the kinds of questions that remain anticipate next year’s math curriculum.
Some teachers might provide time for reflection within the context of an end of unit project, while others may decide to build reflection and review into their students’ daily schedule. Activities could be as simple as a writing assignment in which students explain what they know about fractions, or making a mind map. Longer projects that let students demonstrate what they have learned might include making an illustrated glossary of related vocabulary, or making an instructional video for younger students. Curating a portfolio of their best work would also fit the bill.
Class projects may also be used to give students a chance to revisit what they have learned in a thoughtful manner. Students might contribute to a class recipe book titled ‘Stop & Smell the Fractions.’ Others could create a ‘fraction flower garden.’ Let young students dictate captions explaining how their illustrations show various fractional amounts. The art teacher might help your students recreate florals by famous artists for this purpose.




One-fourth of these hibiscus blossoms are orange. One-eighth of them are yellow.
Help your students explore and understand rational numbers. It is fundamental – not only for their continuing mathematical education but also for their ability to participate in the community after graduation. Start by considering these research-based strategies.
- Have confidence in your own math skills
- Directly compare /contrast integers with rational numbers
- Focus on academic vocabulary
- Use a variety of mathematical manipulatives; especially a number line
- Connect fractions with other subjects
- Invite colleagues & families to lend a hand
- Plan time for students to reflect on the quality of their work
Commit to using all or part of the seven strategies explained above, or other research-based approaches. Keep track of what works best for your students in your unique educational setting.
There are many roads to success.
Share This Story, Choose Your Platform!
Download Colorful Collections:
A Mindful Exploration of Proper Fractions
Help your students make sense of fractions.
I started teaching in 1987, which means I’ve collected many tips and tricks along the way. In this ebook, I share concepts, strategies, and classroom materials to help you make math sticky.
Along with this useful ebook, you will receive weekly emails from StickyMath@UnCommon-Core.com. I send information like: teacher tips, educational ideas, book reviews, curated lists, reviews of educational sites, and free first drafts of products that I’m creating for my TPT store. That way, you get helpful ideas and free stuff, while I get some feedback before I finalize products and put them up for sale.
I value your privacy. I will never sell your information. You may unsubscribe at any time.
All the best!
Isabelle
Isabelle Hoag M. Ed.

