Why is 20% of 50 the same as 50% of 20?

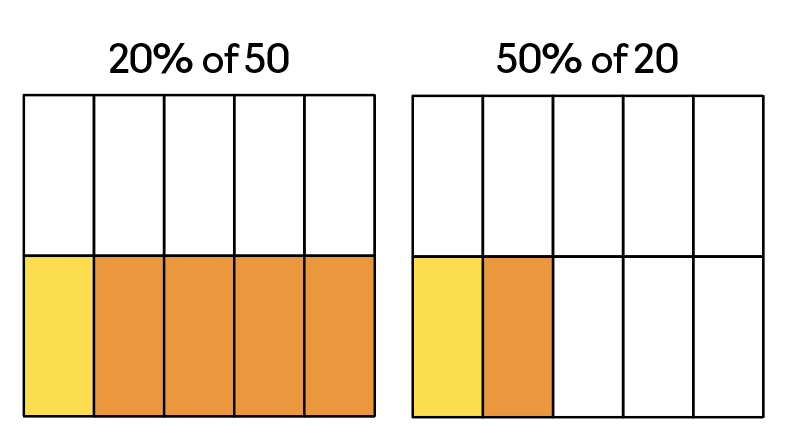
Does the commutative property of multiplication apply to calculating percents?

Yes, fractions are division problems at heart. No, the commutative property doesn’t apply to division. So, how come 20% of 50 is the same amount as 50% of 20?

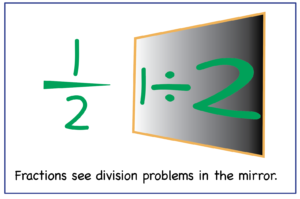
Let’s take a look.

Twenty percent of 50 can be found by multiplying 50 x 20 (1000) and then dividing by 100 to get ten. 

But, it’s much easier to find 50% of 20, isn’t it? Most students automatically know that half of 20 is ten.

Your students will be fascinated to find out that this switcheroo works for all percentages. 

Remind them that the order of factors in multiplication doesn’t change the product. Encourage your students to expand their understanding of the commutative property of multiplication so that it applies to percents.

We want students to be able to think flexibly about percents. We also encourage students to use mental math to calculate percents, so, solving 20% x 50 by flipping it around to 50% of 20 makes sense. 

The Order of Factors Doesn’t Change the Product

Even though the commutative property doesn’t apply to division and there is division in calculating percentages, x% of y will always equal y% of x. This swap works every single time. It makes mental calculations of percentages even easier. 

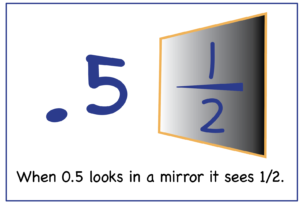
If your students are really worried about applying the commutative property to percents, have them change the percentage to a decimal first then multiply ~ .2 times 50 is the same as .5 times 20. 

At this point, your students may notice that it seems as if they are doing more than changing the order of factors. Are they also changing the magnitude of the factors? 

Look Closely at What is Happening

Let’s unpack the expression: .2 x 50  

Rewrite it like this: .1 x 2 x 5 x 10  

Reorder it like this:  2 x 5 x .1 x 10

Think about one-tenth times ten ~ that boils down to one ~ right? And in multiplication, one doesn’t change anything. So, we’re left with 2 x 5. 

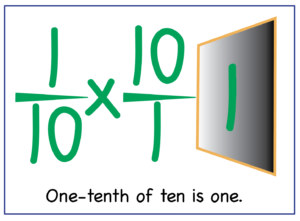
Though it may seem as if swapping .2 x 50 for .5 x 20 is changing more than the order of the factors, when students take a closer look, they will see this is not the case. Eventually, after having seen several examples, they will be able to explain why the commutative property of multiplication applies when calculating percents.

  Practice, Practice, Practice

Challenge students to test as many math problems of this sort as they can think of. 

IF they find an example in which the percents cannot switch places they will be famous the entire world around!! 

Teaching your students to use mental math to calculate percents and to consider swapping the factors around in search of an easier math problem, gives them the tools to understand percents and the ability to think flexibly when solving problems which include them.